The Zen Way
x 1 + y 1 = n 1
Let S ( n ) denote the number of ordered pairs ( x , y ) satisfying the equation above for natural numbers x , y , n with n > 1 . Find the value of S ( 6 ) .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Here is a solution similar to yours. x 1 + y 1 = 6 1 6 x + 6 y = x y 6 x + 6 y − x y − 3 6 = − 3 6 ( B y S F F T ) 6 ( x − 6 ) − y ( x − 6 ) = − 3 6 ( 6 − y ) ( x − 6 ) = − 3 6 ⇒ ( y − 6 ) ( x − 6 ) = 3 6 T h e r e f o r e , t h e s o l u t i o n s a r e ( 4 2 , 7 ) , ( 7 , 4 2 ) , ( 2 4 , 8 ) , ( 8 , 2 4 ) , ( 1 8 , 9 ) , ( 9 , 1 8 ) , ( 1 5 , 1 0 ) , ( 1 0 , 1 5 ) a n d ( 6 , 6 ) .
If I were clever or sophisticated I wouldn't do this. However, I wanted to see how the numbers roll out. Both x and y must be greater than or equal to n . I therefore wrote a little code to write out values of these variables that satisfy this equation. Here's what I saw:
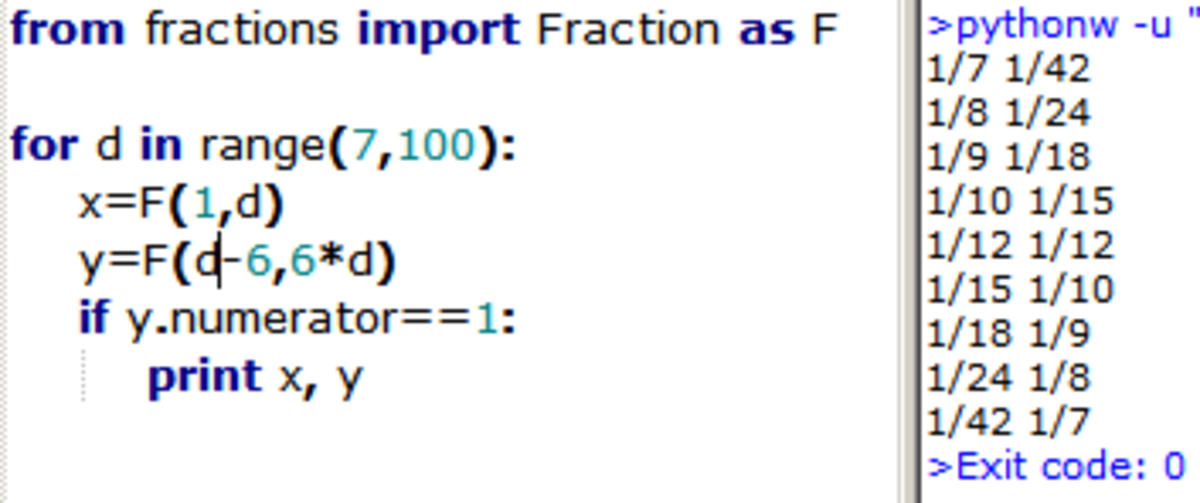
Obviously not a proof, but gives me the intuition I always like to have.
rearranging (1/x)+(1/y)=(1/6) we get xy-6y-6x=0. Now we consider simons favourite factorizing trick. We write this as xy-6y-6x+36-36=0. Hence (x-6)(y-6)=36. Now we think combinatorially. The number of distinct pairs of solutions is equal to the number of possible values of x-6 to satisfy the equation since for each distinct (x-6) there cannot be 2 distinct values of (y-6) since it would contradict the equation. Now 36 =(2^2)(3^2). The number of distinct solutions is (2+1)(2+1)=9 by using the fact that if there are n distinct primes appearing x1,x2...xn times respectively the total number of results is (x1+1)(x2+1)...(xn+1)