What identity can I use?

We know the identity, $(a-b)^3=a^3-b^3-3ab(a-b)$

Substituting the values $\color{#EC7300}{(a-b)=4}$ and $\color{#20A900}{ab=45}$ in the identity, we get: $4^3=a^3-b^3-3\color{#20A900}{(45)}\color{#EC7300}{(4)} \\ a^3-b^3=4^3+3\color{#20A900}{(45)}\color{#EC7300}{(4)} \\ a^3-b^3=64+540\\ a^3-b^3=\boxed{604}$

We have, $a^3- b^3= ( a - b )(a^2 + ab + b^2 ),$
$a^3 - b^3 = ( a - b ) ( a^2 - 2ab + b^2 + 2ab + ab ),$
$a^3 - b^3 = ( a - b ) { ( a - b ) ^2 + 3ab },$
$a^3- b^3 = 4*( 4^2 + 3* 45 ) = 4* ( 16+135)$
$= 4 * 151 = 604.$
Ans is 604.

If you find this question interesting, like or share.

First, let square both sides of the equation a - b = 4, which we have

(a-b)^2 = 16

a^2 - 2ab + b^2 = 16

a^2 + b^2 = 16 + 2ab

a^2 + b^2 = 106 (ab =45)

Next, evaluate a^3 - b^3

a^3 - b^3 = (a-b)(a^2 + ab + b^2)

a^3 - b^3 = (a-b)(a^2 + b^2 + ab)

a^3 - b^3 = 4(106 +45)

a^3 - b^3 = 4(151)

a^3 - b^3 = 604

a - b = 4, a*b = 45 => a = 9, b = 5 => a^3 - b^3 = 726 - 125 = 604...

$( a - b ) = 4 , ab = 45 , 2( ab ) = 90$

$( a - b )^2 = a^2 - 2( ab ) + b^2 , ( a - b )^2 = (4)^2 = 16$

$a^2 - 2( ab) + b^2 = 16$

$a^2 + b^2 = 16 + 2( ab ) = 16 + 90 = 106$

$a^3 - b^3 = ( a - b ) ( a^2 + ab + b^2 )$

Replace everything and: $a^3 - b^3 = ( 4 ) ( 106 + 45 ) = ( 4 ) ( 151 ) = \boxed{604}$

Given a - b = 4 and ab = 45, Evaluate $a^{3} - b^{3}$

Solve both sides for a, gives a = 4 + b and a = 45 / b

Therefore 4 + b = 45 / b

Multiply both sides by b gives $4b + b^{2} = 45$

Subtract 45 from both sides gives $b^{2}$ + 4b- 45 = 0

Factoring gives ( b + 9 )( b - 5 ) = 0

Therefore b = -9 or b = 5

Substitute b in ab = 45 results in: a(-9) = 45, a = -5 or a(5) = 45, a = 9

Solve $a^{3} - b^{3}$ by substitution of ( a, b ): ( -5, -9 ) or ( 9, 5 )

Results in:

$(-5)^{3} - (-9)^{3}$ = -125 - ( -729 ) = 604

or

$(9)^{3} - (5)^{3}$ = 729 - 125 = 604

Therefore $a^{3} - b^{3}$ = $\boxed {604}$

$a^3-b^3=(a-b)(a^2+ab+b^2)=(a-b)[(a-b)^2+3ab]$

Subbing in $a-b=4$ and $ab=45$

$a^3-b^3=4\times(4^2+3\times45)=\boxed{604}$

$a^3-b^3=(a-b)^3+3ab(a-b)$

or, $a^3-b^3=4^3+3 \times 45\times4$ ...........[values are given]

or, $a^3-b^3=64+540=604$

$a - b = 4$ $ab = 45$ $a^3 - b^3 = ?$ $(a - b)^3 = a^3 - 3a^2 b + 3ab^2 - b^3$ $a^3 - b^3 = (a - b)^3 + 3a^2 b - 3ab^2$ $a^3 - b^3 = (a - b)^3 + 3(a^2 b - ab^2)$ $a^3 - b^3 = (a - b)^3 + 3(a - b)ab$ $a^3 - b^3 = (4)^3 + 3(4)45$ $a^3 - b^3 = 64 + 540$ $a^3 - b^3 = 604$

$a-b=4...(i)$

$ab=45...(ii)$

From $(i),$

$a=b+4$

Substituting the value in $(ii),$

$(b+4)(b)=45=9*5$

Hence, $b$ comes out to be 5

$a=b+4=5+4=9$

$a^3-b^3=729-125=604$

Hence, the answer is $604$

In this solution, letters $a$ and $b$ are changed to $m$ and $n$ , because I used quadratic equation formula, where $a$ , $b$ and $c$ appear.

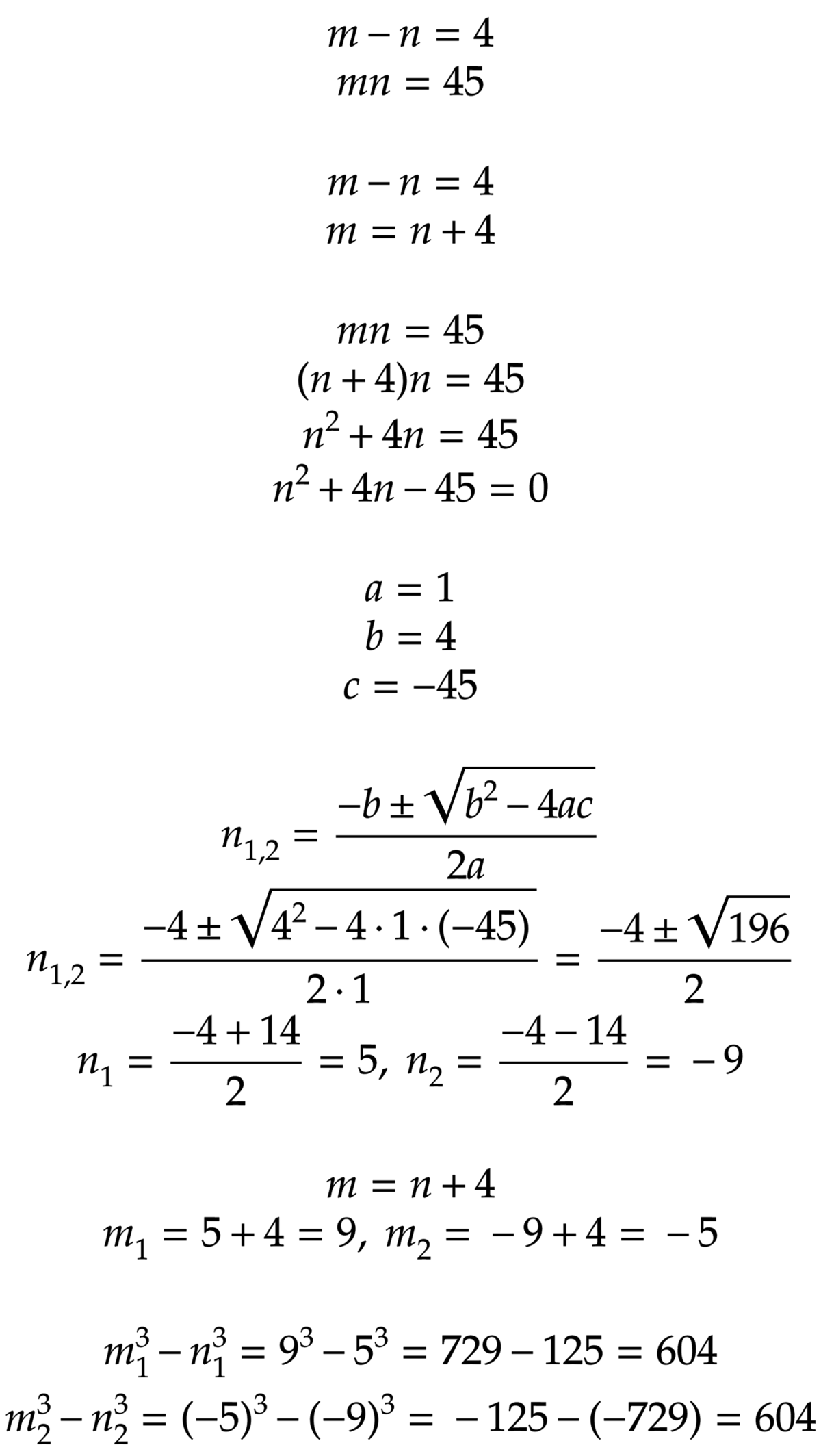
The solution is 604.

I noticed that $a = 9$ and $b = 5$ are one of the solutions to the problem. So I subtracted $125$ from $729$ to get $\boxed{604}$ . I know that this is not the correct way, but still it works!😉

$\begin{aligned} { (a-b })^{ 3 } & = & { a }^{ 3 }-3{ a }^{ 2 }b+3a{ b }^{ 2 }-{ b }^{ 3 } \\ { 4 }^{ 3 } & = & { a }^{ 3 }-{ b }^{ 3 }-3ab(a-b) \\ { a }^{ 3 }-{ b }^{ 3 } & = & 64+3(45)(4) \\ \quad & = & \boxed { 604 } \end{aligned}$

a^3 - b^3 = (a b)[(a - b)^2 + 3ab) = (4)[(16 + 3(45] = 4 (16 + (3)(45)] = 4 151 = 604.

$\begin{aligned} a^3-b^3 & = (a-b)\left(a^2+ab+b^2\right) \\ & = (a-b)\left(a^2-2ab+b^2+3ab \right) \\ & = (a-b)\left((a-b)^2+3ab \right) \\ & = 4\left((4)^2+3(45) \right) \\ & = 4\left(16+135 \right) \\ & = \boxed{604} \end{aligned}$

Since $ab = 45$ , it is clear that at least one variable must be $5$ , since $5$ and it's multiples are the only numbers to have $5$ as the last digit in their product.

For the sake of the first equation, let's conclude that $b = 5$ and therefore $\rightarrow a = 4+5 = 9$ .

After plugging in, we get that: $9^3 - 5^3 = 729 - 125 = \boxed{604}$

$a-b = 4$ and $ab = 45$

The formula that we are mainly going to use is this one:

$(x-y)^3 = x^3-3x^2y+3xy^2-y^3$

But this can be simplified as $(x-y)^3+3xy(x+y)$

In our case the formula becomes : $(a-b)^3+3ab(a+b)$

So : $(4^3)+3(45)(4)$

$(64)+ (540)$

$=604$

For more information: visit the Algebraic Manipulation

Since $a^3 - b^3 = (a-b)^3 + 3ab(a-b)$

Substituting $a-b = 4$ and $ab = 45$

We get $a^3 - b^3 = 604$

find the factors of 45 that is 3 5 9 15 now search for the 2 values that have 4 difference between them so they are 9 and 5 now 9^3 - 5^3=604

1st solution, ab=45,a-b=4,a-(45÷a)=4,,,,,,,,,,,a^2 -4a-45=0,a=root of equation ,a=9 or -5,b=5 or -9,so a^3 -b^3 =9^3-5^3=604.####################.another solution,,, (a-b)^3=a^3 -b^3 -2a^2b+2b^2a+ab^2 -a^2b ,a-b=4,,,64=a^3 -b^3 -3a^2b+3ab^2,64=a^3 -b^3+3ab(b-a),ab=45,a^3-b^3=64+3×4×45=604####

a^3-b^3= (a-b)^3+3ab(a-b) Substituting the values a-b=4 and ab=45 in the identity, we get:

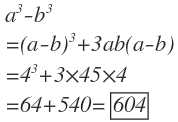
(a-b)=4 cubing both side a^3-b^3-3ab(a-b)=64 then a^3-b^3-3 45 4=64 so a^3-b^3=604