Can you make it larger?
2 1 + 3 1 + 4 1 + … + 1 0 0 0 0 1
What is the greatest positive integer less than equals to the number above?
Share if you like.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Good work sir ! :)
I didn't follow it. can you Plz explain?
Log in to reply
Yes, it is difficult to show with a short explanation. I have amended the diagram and explain more in the solution.
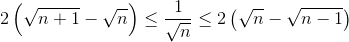
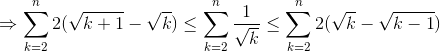
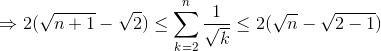
We know that S = k = 2 ∑ 1 0 0 0 0 k 1 ≈ I = ∫ 2 1 0 0 0 0 x 1 d x = 1 9 7 . 1 7 1 5 7 2 9 .
In the graphs above, S is represented by total area of the vertical bars and I is the area under the curve x 1 .
Looking at the left graph, the first bar of S centers at x = 1 . If we remove the area of half of the first bar ( 2 1 × 2 1 ) and half of last bar ( 1 0 0 0 0 1 × 2 1 ) (not shown in the graph), we note that:
S − 2 1 × 2 1 − 2 1 × 1 0 0 0 0 1 > I
This is because the small area a of each bar is larger than the area b that follows.
⇒ S > I + 2 1 ( 2 1 + 1 0 0 1 ) = 1 9 7 . 5 3 0 1 2 6 3
Looking at the right graph, where the first bar of S centers at x = 0 . 5 , we note that S without the first bar is smaller than I :
⇒ S − 2 1 < I
This is because all a = 0 .
⇒ S < 2 1 + I = 1 9 7 . 8 7 8 6 7 9 7
Therefore,
1 9 7 . 5 3 0 1 2 6 3 < S < 1 9 7 . 8 7 8 6 7 9 7 ⇒ ⌊ S ⌋ = 1 9 7