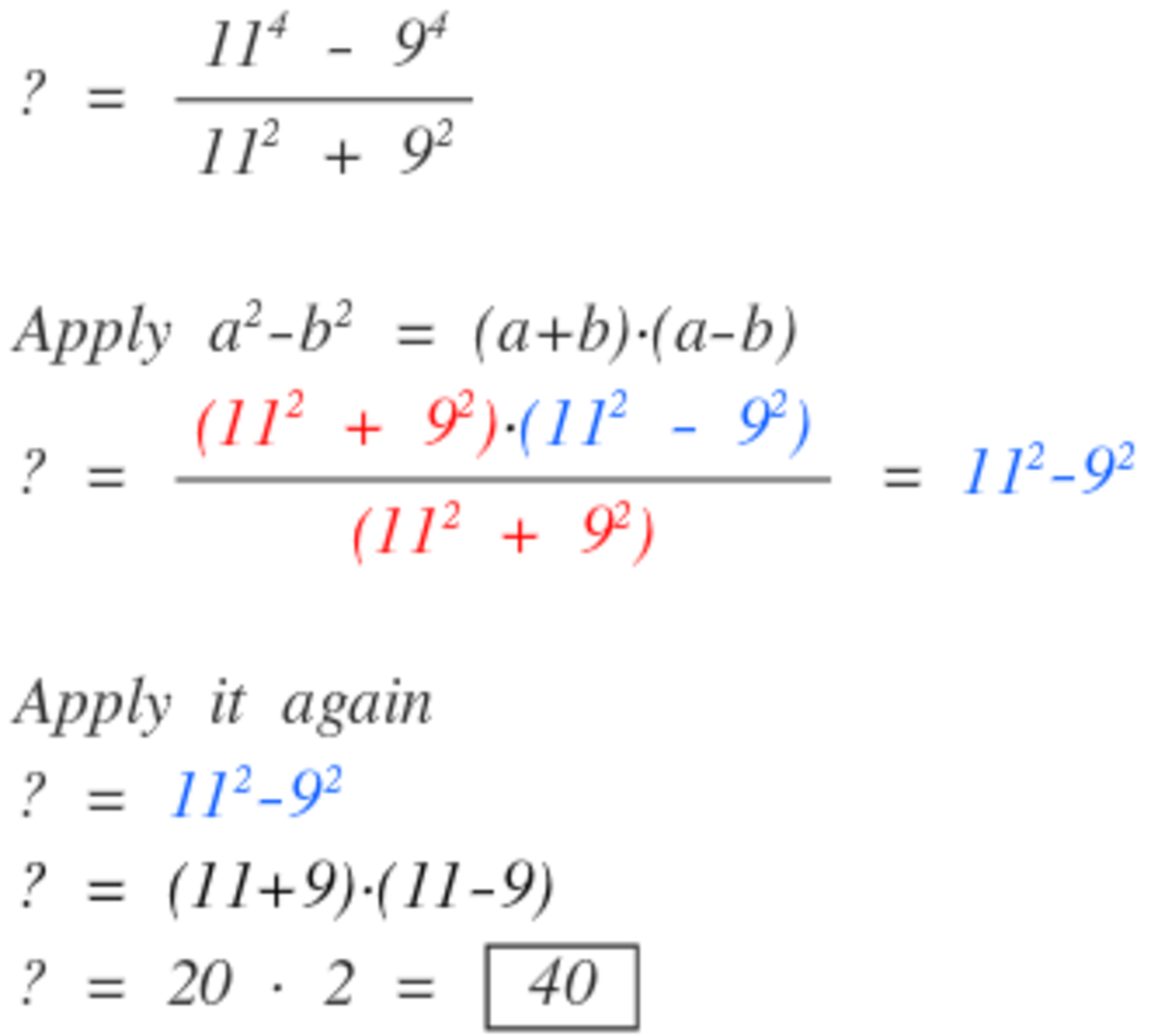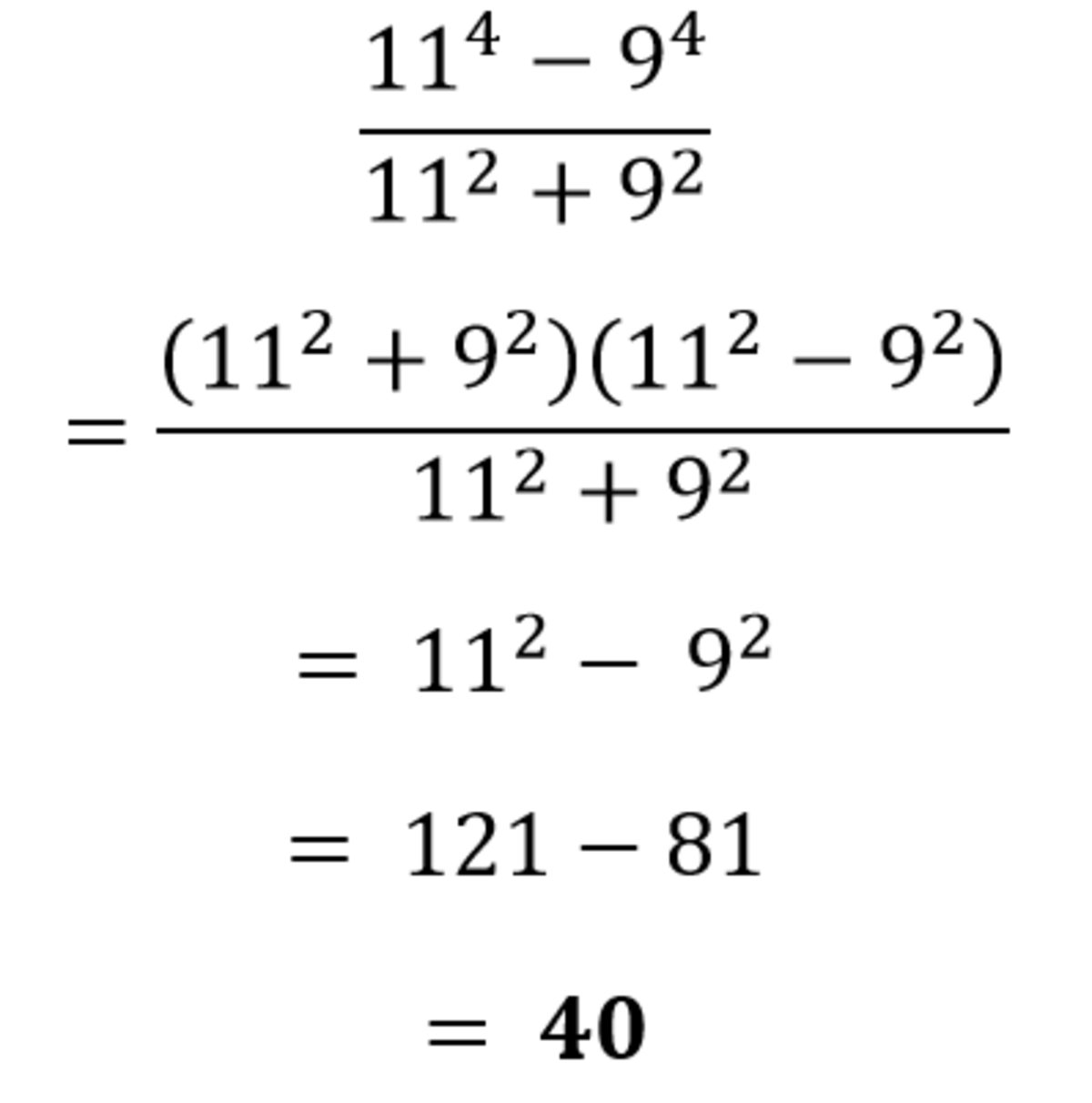This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
really Llewellyn you made me understood well and i am acknowledging you so much
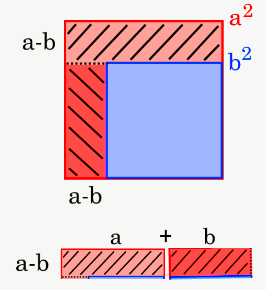
Using the identity, ( a 2 − b 2 ) = ( a + b ) ( a − b ) , the fraction can be easily factorized and solved.
1
1
2
+
9
2
1
1
4
−
9
4
=
1
1
2
+
9
2
(
1
1
2
+
9
2
)
(
1
1
2
−
9
2
)
=
1
1
2
−
9
2
=
(
1
1
+
9
)
(
1
1
−
9
)
=
2
0
×
2
=
4
0
But how do you go from (11²-9²)=20x2? Shouldn't it be (11²-9²) = (121-81) = 40? I know they're the same answer but where did that 20x2 come from?
Log in to reply
It's factorised. (a2-b2) = (a+b)(a-b) = (20)(2)
Log in to reply
Yes, using that factorization many times :) That's what I liked about this problem.
(Of course, one could expand out everything, but that's not the point.)
here again they have used the formula (a^2 - b^2) = (a+b)(a-b) i.e (11+9)(11-9) = 20x2 =40
Please scroll left
He got (11+9) which is equal to 20 and then he got (11-9) which is equal to 2 so he got (20)(2) which is just 20*2 which is equal to 40.
Yes, essentially they are just factoring one too many times to make it confusing. After you are at 11^2 - 9^2, you could just as easily say 11^2 = 121 and 9^2 = 81 so 121-81 = 40. They were trying to get you to use the "rules" for factoring/ FOIL etc. when in this specific case it would still be practical to just solve as I showed above.
From (11^2-9^2)==(11+9)×(11-9)=20×2=40 Now u get it??
a^2-b^2 = (a+b)(a-b). So (11^2-9^2) = (11+9)(11-9), which also equals (20)(2) because of PEMDAS: basically do the operations within the parentheses, and finally multiply.
Quite easy x^4-y^4/x^2+y^2 = (x^2-y^2)(x^2+y^2)/(x^2+x^2)= x^2-y^2 Put values and get the ans
yes, and we could use it once more, to make it easier to calculate :)
11^4-9^4=
(11)^2-(9)^2
=(11^2+9^2)(11^2-9^2) [a^2-b^2=(a+b)(a-b)]
so,(11^2+9^2)(11^2-9^2)/(11^2+9^2)
=11^2-9^2
=121-81
40
(11^4-9^4)/11^2+9^2=(11^2-9^2) (11^2+9^2)/(11^2+9^2)=(11^2-9^2) =(11+9) (11-9)=20*2=40
I thought it is 11^4-9^4=2^4 and 11^2+9^2=20^2 and simplify 2^4/20^2, simplify again 2^2/20 =4/20 or 1/5.. my answer is 1/5, andi think all answers are wrong, this is only my idea, correct me if im wrong... thanks
Log in to reply
One easy way to show that it isn't correct is to use smaller values e.g. 3^4 - 2^4. From your solution, the answer would be 3^4 - 2^4 = 1^4=1. However, 3^4 = 81 and 2^4 = 16. Therefore 3^4 - 2^4 = 81 - 16 = 65. You can now see that your method wouldn't work. Also, it can be simplified as 3^4 - 2^4 = (3^2 - 2^2)(3^2 + 2^2) = (9 - 4)(9 + 4) = 5 x 13 = 65. Re-solve the question using this method
No, look up Rules of Exponents . You are saying that a n − b n = ( a − b ) n and a n + b n = ( a + b ) n , neither of which is true.
Log in to reply
I think that you are right.. The answers above, of the exercise are wrong.. It should be 4 the final result.
a² - b²= (a+b)(a-b) So . 11⁴ — 9⁴ ÷ 11²+9²= (11²—9²)(11²+9²)÷(11²+9²) = 11²—9² =121—81 =40
1 1 2 + 9 2 1 1 4 − 9 4 = 1 1 2 + 9 2 ( 1 1 2 − 9 2 ) ( 1 1 2 + 9 2 ) = 1 1 2 − 9 2 = 1 2 1 − 8 1 = 4 0
11^4-9^4/11^2+9^2 = (14641-6561)/(121+81) = 8080/202=40
I know this isn't the prettiest way to do it at, but brute force works most of the times. ;)
11^4 / 11^2 = 11^2
-9^4 / 9^2 = -9^2
11^2 - 9^2 = 121 - 81 = 40
cut the same terms, the remaining is 11^2-9^2 which is equal to 40 And that's Answer.....thanks!
(11^4 - 9^4)/(11^2 + 9^2) = {(11^2 - 9^2). (11^2 + 9^2)}/(11^2 - 9^2) = 11^2 + 9^2 = 121 - 81 = 40
(11² + 9²)x(11² - 9²)/(11² + 9²) = 11² - 9² = (11+9)(11-9) = 20x2 = 40
Using the difference of two squares identity, we know that 1 1 4 − 9 4 = ( 1 1 2 + 9 2 ) ( 1 1 2 − 9 2 ) . Because the ( 1 1 2 + 9 2 ) cancel, we are left with ( 1 1 2 − 9 2 ) , or 40.
That's nice :)
[(11^2+9^2)(11^2-9^2)]/(11^2+9^2) =(11^2-9^2) =40
That's nice :)
We knw dat a^2 -b^2= (a+b)(a-b).. use the identity and solve it...
Yes indeed. Can you add more details?
(11^4-9^4)/(11^2+9^2)=11^2-9^2 =(11+9)(11-9)=20×2=40
11^2^2-9^2^2/11^2+9^2 =(11^2+9^2)(11^2-9^2)/11^2+9^2) =11^2-9^2 =121-81 =40