Factor Me!
( 2 0 0 7 × 2 0 0 6 2 0 0 6 ) − ( 2 0 0 6 × 2 0 0 7 2 0 0 7 ) = ?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
24 solutions
Excellent answer
Log in to reply
but we can't think 20062006 or 20072007 is multiply state. we think that is an integer number...
I liked that method.
Brilliant dude
What is it with variable substitution other than numerical, nowadays? Anyway, great answer!
but we can't think 20062006 or 20072007 is multiply state. we think that is an integer number...
Log in to reply
20072007 = 2007 * 10000 + 2007 = 2007 * 10001 20062006 = 2006 * 10000 + 2006 = 2006 * 10001
2 0 0 7 × 2 0 0 6 2 0 0 6 − 2 0 0 6 × 2 0 0 7 2 0 0 7
= ( 2 0 0 6 + 1 ) × 2 0 0 6 2 0 0 6 − 2 0 0 6 × ( 2 0 0 6 2 0 0 6 + 1 0 0 0 1 )
= 2 0 0 6 × 2 0 0 6 2 0 0 6 + 2 0 0 6 2 0 0 6 − 2 0 0 6 × 2 0 0 6 2 0 0 6 − 2 0 0 6 2 0 0 6
= 0
A simpler approach would be to factorize like this,
2 0 0 7 × 2 0 0 6 × ( 1 0 0 0 1 − 1 0 0 0 1 ) = 2 0 0 7 × 2 0 0 6 × 0 = 0
Log in to reply
Oh right! Good thinking :)
Without useing calculator
i thought 20062006 was 2006^2 !!
2007 x 20062006 - 2006 x 20072007
= 2007 x 2006 x 10001 - 2006 x 2007 x 10001
= 0
brilliant...
I like this one
(2007x20062006) - (2006x20072007) = (2006 + 1) (20062006) - 2006 (20062006 +10001) =2006 x 20062006 + 20062006 - 2006 x 20062006 - 20062006 = 0.
DON'T YOU THINK ITS TOO COMPLICATED ...........
BUT GOOD APPROACH AND THINKING
excelent...
2007 x 20062006 - 2006 x 20072007
= (2007 x 2006 x 10001) -( 2006 x 2007 x 10001)
= 0
You may check for any errors, but this is how I perceived this would be solved.

2007=2.007×10^3 ,,20062006=2.0062006×10^7 ,, 2006=2.006×10^3 ,,20072007=2.0072007×10^7,,so formula=2.007×10^3×2.0062006×10^7-2.006×10^3×2.0072007×10^7=10^10×(2.007×2.0062006-2.006×2.0072007),=10^10×(2.007×~2.006-2.006×~2.007)=0×10^10=0####
( 2007 * 20062006 ) - ( 20072007 * 2006 )=
( 2007 * 10001 * 2006 )- ( 2007 * 10001 * 2006 )=
2007 * 10001 * 2006 ( 1 - 1 )=
[ TAKING 2007 * 10001 * 2006 AS COMMON ]
2007 * 10001 * 2006 * 0=
0
= 2 0 0 7 × 2 0 0 6 2 0 0 6 − 2 0 0 6 × 2 0 0 7 2 0 0 7 = 2 0 0 7 × 2 0 0 6 × 1 0 0 0 1 − 2 0 0 6 × 2 0 0 7 × 1 0 0 0 1 = 0
Solve: ( 2 0 0 7 × 2 0 0 6 2 0 0 6 ) − ( 2 0 0 6 × 2 0 0 7 2 0 0 7 ) = x
Multiply the expression by 2 0 0 6 × 2 0 0 7 2 0 0 6 × 2 0 0 7 i.e. just multiply by 1 , so nothing changes.
2 0 0 6 × 2 0 0 7 2 0 0 6 × 2 0 0 7 ( ( 2 0 0 7 × 2 0 0 6 2 0 0 6 ) − ( 2 0 0 6 × 2 0 0 7 2 0 0 7 ) ) = x
2 0 0 7 in the denominator cancels:
2 0 0 6 2 0 0 6 × 2 0 0 7 ( ( 2 0 0 6 2 0 0 6 ) − ( 2 0 0 6 × 1 0 0 0 1 ) ) = x
2 0 0 6 in the denominator also cancels:
1 2 0 0 6 × 2 0 0 7 ( ( 1 0 0 0 1 ) − ( 1 0 0 0 1 ) ) = x
So we're left with:
2 0 0 6 × 2 0 0 7 ( 1 0 0 0 1 − 1 0 0 0 1 ) = x
The bit in parenthesis is 0 , so:
2 0 0 6 × 2 0 0 7 ( 0 ) = x
0 = x
( 2 0 0 7 × 2 0 0 6 2 0 0 6 ) − ( 2 0 0 6 × 2 0 0 7 2 0 0 7 ) = ( 2 0 0 7 × ( 2 0 0 7 2 0 0 7 − 1 0 0 0 1 ) ) − ( ( 2 0 0 7 − 1 ) × 2 0 0 7 2 0 0 7 ) = ( 2 0 0 7 × 2 0 0 7 2 0 0 7 − 2 0 0 7 × 1 0 0 0 1 ) − ( 2 0 0 7 × 2 0 0 7 2 0 0 7 − 2 0 0 7 ) = ( 2 0 0 7 × ( 2 0 0 7 2 0 0 7 − 1 ) ) − ( 2 0 0 7 × ( 2 0 0 7 2 0 0 7 − 1 ) ) = ( 2 0 0 7 × 2 0 0 7 2 0 0 6 ) − ( 2 0 0 7 × 2 0 0 7 2 0 0 6 )
I need to know how 10001 caluclated ?!
2007 x 20062006 = 2007 x 2006 x 10001 2006 x 20072007 = 2006 x 2007 x 10001
Therefore, the answer is 0
(2007)(20062006) - (2006)(20072007)
=(2007)(20072007-10001) - (2006(20072007)
=(2007)(20072007) - (2007)(10001) - (2006)(20072007)
=20072007 - (2007)(10001)
=20072007 - (2007)(10000+1)
=20072007 - 20072007
=0
Moderator note:
Good approach of comparing to 2 0 0 7 × 2 0 0 7 2 0 0 7 .
(2007 * 2006)-(2006 * 2007) due to commutative the answer is 0
2007 x 20062006 - 2006 x 20072007
=2007 x (10001 x 2006) - 2006 x (10001 x 2007) = 0
( 2007 × 20062006 ) - ( 2006 × 20072007 ) = ( 2007 × 20062006 ) - 2006 ( 20062006 + 10001 ) = ( 2007 × 20062006 ) - ( 2006 × 20062006 ) - ( 2006 × 10001 ) = 20062006 ( 2007 - 2006 ) - ( 2006 × 10001 ) = 20062006 ( 1 ) - ( 20062006 ) = 0
simplify it to be
( 2 0 0 7 × 1 0 0 0 1 × 2 0 0 6 ) − ( 2 0 0 6 × 1 0 0 0 1 × 2 0 0 7 )
= 0
A very interesting observation is that when 101, containing one cipher between two 1's, is multiplied by a two-digit number, we obtain the latter repeated as xx to xxxx. Similarly, xxx * 1001 = xxxx. So, xxxx * 10001 = xxxxxxxx.
This means, 20062006 = 2006 * 10001 20071007 = 2007 * 10001.
Thus, the answer is Cipher. :D
basically it's this:
A = 2007 and B = 2006 ;
20062006 = 2006 * 10001
20072007 = 2007 * 10001;
Therefore ( the equation is thus ) (A * 10001 B) - ( B 10001 A ) factor out the 10001 and you are left with ( a b ) - (b*a ) ==> 0
It works starting with 1 digit numbers ..
A= 7, B = 9
7
99 - 99
7 = 0
(A
11
B) - ( B
11
A)
AB - BA ==> 0
(2007x20062006)-(2006x20072007)=(2007x2006+2007x2006x10^4)-(2006x2007+2006x2007x10^4)=0
if x=2007 and y=2006
then x(10001y)-y(10001x) = 10001xy - 10001xy = 0 (Ans)
2007 x 20062006 - 2006 x 20072007.
= 40264446042 - 40264446042
= 0
Moderator note:
Although you got the right answer, it is very impractical to calculate multiplication of 2 relatively large numbers... twice.
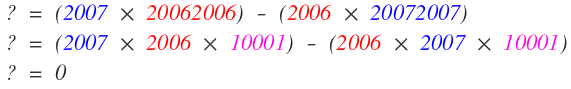
Assume a=2007, b=2006
And then our equation becomes:
a × 1 0 0 0 1 b − b × 1 0 0 0 1 a = 1 0 0 0 1 a b − 1 0 0 0 1 a b = 0