So many fives
How many integers between 1 and 1,000,000 contain the digit 5 at least twice?
The answer is 114265.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
I did the same way :D
1000000 is the only number in the given range with more than 6 digits and it doesn't contain two or more 5s so we can discount it. We then can treat all the other numbers as 6 digit numbers, some of which will have zeros as some of their earlier digits.
Case 1: Exactly two fives
There are 6C2 ways to position the two fives and 9 choices for each of the other four digits (0,1,2,3,4,6,7,8 or 9) so there are:
(6C2 x 9 4 ) = 98415 ways to do this
Case 2: Exactly three fives
There are 6C3 ways to position the fives and 9 choices for each of the other four digits:
(6C3 x 9 3 ) = 14580 numbers
Case 3: Exactly four fives
In the same way as above:
(6C4 x 9 2 ) = 1215 numbers
Case 4 : Exactly five fives
(6C5 x 9) = 54
Case 5: Exactly five fives:
1 number
So in total there are 98415 + 14580 + 1215 + 54 + 1= 1 1 4 2 6 5 numbers.
Thanks for your detailed solution.
- Numbers contain digit 5 at least Twice is the difference between total numbers contain digit 5 and numbers contain digit 5 Once.
- Total Numbers = 1 0 6
- Numbers doesn't contain digit 5 = 9 6
- Total Numbers contain digit 5 = 1 0 6 - 9 6 = 468559
- Numbers contain digit 5 Once = ( 1 6 ) 9 5 = 354294
⇒ Numbers contain digit 5 at least Twice = 468559 - 354294 = 1 1 4 2 6 5
10^6 cannot be the total nos. because the question range is btw 1 to 1000000. if u include 10^6 which mean that 000000 is also possible. correct me if i am wrong
As 0 and 1000000 have the same properties → (they don't contain digit 5) , so i replaced 1000000 with 0 and calculated between { 0 and 999999 }.
- [1 , 1000000] inclusive = [0 , 999999] inclusive = 1 0 6 numbers
-
(1 , 1000000) exclusive = (0 , 999999) exclusive = 1 0 6 -2 numbers
-
I solved it inclusive [1 , 1000000] = [0 , 999999] = 1 0 6 numbers
-
Total Numbers contain digit 5 = 1 0 6 - 9 6 = 4 6 8 5 5 9
-
If you solve it exclusive (1 , 1000000) = (0 , 999999) = 1 0 6 -2 numbers
-
Total Numbers contain digit 5 = ( 1 0 6 -2) - ( 9 6 -2) = 1 0 6 - 9 6 = 4 6 8 5 5 9
-
Solving this problem inclusive or exclusive doesn't matter as { 1 and 1000000 } or { 0 and 999999 } don't contain digit 5. Remember I only need step 3 (Total Numbers contain digit 5) . No matter what you do, they will cancel each other in Step 3.
Why would you not count 5 in these cases the actual answer is 144568 we must include the 5 too
Because I have counted each different number of fives as a separate case. So for example in case 1 there is exactly two fives so none of the other digits can be a five as well because then there would be more than two fives and therefore that number would be counted again in a later case.
Hope that makes sense now
Python:
1 2 3 4 5 6 7 8 9 |
|
PHP:
<?php
$counter = 0;
for ($i=1;$i<=1000000;$i++)
{
if (substr_count($i, '5') >= 2)
$counter++;
}
echo $counter;
?>
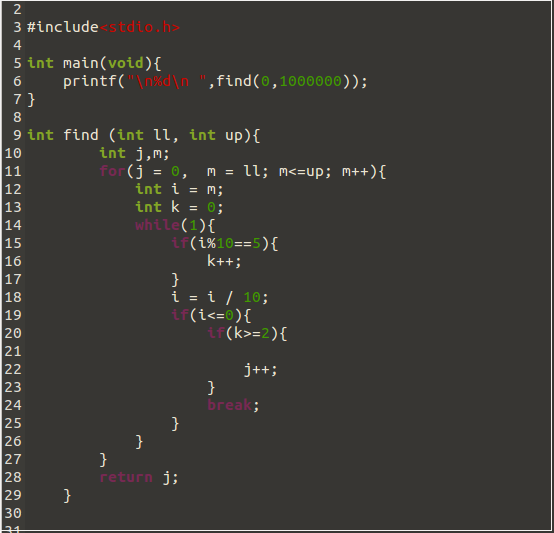
Why don't we think it other way...I mean instead we can find the total number that DON'T have at least 2 FIVES and SUBTRACT it from ONE MILLION.
Case 1, no 5's: There 6 positions and 9 digits left, so this is 9^6=531441
Case 2, exactly 1 five:Choosing the position for this one 5 is 6C1 and there are 5 positions left with 9 choices of digits.So number of numbers that has exactly one 5 = 6C1*9^5 =354294 Now 1,000,000 - 885735 = 114265