How fast can you multiply?

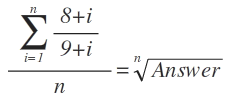
$\large \textrm{An informal solution:}$

Expanding out the expression gives us,

$\frac{9}{10}\times \frac{10}{11}\times \cdots \times \frac{98}{99}\times \frac{99}{100}$

After cancellation of like terms, we are left with the answer $\dfrac{9}{100}=\boxed{0.09}$

---

$\large \textrm{The same solution (Presented in a formal manner):}$

The given product can be expressed and evaluated using product notation as follows:

$\displaystyle \prod_{i=10}^{100} \left(1-\dfrac{1}{i}\right)=\displaystyle \prod_{i=10}^{100} \left(\dfrac{i-1}{i}\right)=\frac{\displaystyle \prod_{i=10}^{100}\left(i-1\right)}{\displaystyle \prod_{i=10}^{100}i}=\frac{9\times \displaystyle \prod_{i=10}^{99}i}{100\times \displaystyle \prod_{i=10}^{99}i}=\dfrac{9}{100}=\boxed{0.09}$

( $1-1/10)(1-1/11)(1-1/12)...(1-1/99)(1-1/100)=\\ \left( \frac { 9 }{ 10 } \right) \left( \frac { 10 }{ 11 } \right) \left( \frac { 11 }{ 12 } \right) ...\left( \frac { 98 }{ 99 } \right) \left( \frac { 99 }{ 100 } \right) =\\ \frac { 99\times 98\times 97\times ...10\times 9 }{ 100\times 99\times 98\times ...11\times 10 } =\\ \frac { \frac { 99! }{ 8! } }{ \frac { 100! }{ 9! } } =\quad \frac { 99!9! }{ 100!8! } \quad =\quad { 0.09 }$

the given sequence can be written as:
(9/10)(10/11)(11/12)........(98/99)(99/100)
= 9/100 = 0.09

=(1 - 1/10)(1 - 1/11)(1 - 1/12)...(1 - 1/99)(1 - 1/100) = (9/10)(10/11)(11/12)...(98/99)(99/100) = 9/100 : simplify final answer=0.09

It's a telescopic sequence once simplified.

Another Solution (By using AM-GM inequalities)

let $a_{i}$ = (1- $\frac{1}{9+i}$ ) this simplifies to $a_{i}$ = ( $\frac{8+i}{9+i}$ )

n=91