Is it a polynomial?
Define a function f : R → R such that f ( f ( x ) ) = x 2 − x + 1 for all real x .
Evaluate f ( 0 ) = ? .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Moderator note:
There are infinitely many solutions to this functional equation. Can you find one?
Hint:
1.
f
(
x
)
=
f
(
1
−
x
)
2. If
f
(
x
)
=
y
, what can we say about
f
(
y
)
?
Note: Almost all of the following solutions are wrong, so read carefully and try and figure out the mistake that was made.
let Y = f ( x ) f ( f ( Y ) ) f ( f ( f ( x ) ) ) f ( x 2 − x + 1 ) = Y 2 − Y + 1 = f ( x ) 2 − f ( x ) + 1 = f ( x ) 2 − f ( x ) + 1 we need f ( 0 ) let try f ( 0 2 − 0 + 1 ) f ( 1 ) = f ( 0 ) 2 − f ( 0 ) + 1 = f ( 0 ) 2 − f ( 0 ) + 1 now we find f ( 1 ) for left side f ( 1 2 − 1 + 1 ) = f ( 1 ) 2 − f ( 1 ) + 1 f ( 1 ) = f ( 1 ) 2 − f ( 1 ) + 1 assign Z = f ( 1 ) so Z 0 = Z 2 − Z + 1 = Z 2 − 2 Z + 1 = ( Z − 1 ) 2 then Z = f ( 1 ) = 1
set back to above equation f ( 1 ) 1 0 f ( 0 ) = f ( 0 ) 2 − f ( 0 ) + 1 = f ( 0 ) 2 − f ( 0 ) + 1 = f ( 0 ) 2 − f ( 0 ) = 0 , 1 but f ( f ( 0 ) ) = 1 so f ( 0 ) can not be 0
finally we get only f ( 0 ) = 1
Hebat ivan
Currently, this is the only correct solution to this problem. Nice solution.
I might disagree with you but i cant deny to you .. i found the answer .. but i also tried to find the function itself. . I have not reached the solution but i think i am mid way. Kinda help me. We take the intial function as (X^1/2)^2 + something I am not able to find that something.. please help
Log in to reply
Such function cannot be the answer, since that means f is linear. If any, f ( x ) would be in the form of something like x 2 + something , but then it's not defined for x < 0 .
Absolute and nice solution.
Nice solution, Upvoted!
nice solution
the best! youre the BEST
Putting x = 0 We get f ( f ( 0 ) ) = 1
But f ( f ( 0 ) ) = f ( 0 ) 2 − f ( 0 ) + 1 = 1 ⟹ f ( 0 ) ( f ( 0 ) − 1 ) = 0
So f ( 0 ) = 1 , 0 ,but f ( 0 ) Can not be 0 ,otherwise there will be divergence in the mapping of the function, so f ( 0 ) = 1
Moderator note:
As pointed out, the function is not
f ( x ) = x 2 − x + 1
Could you explain how you got the equation f ( f ( 0 ) ) = f ( 0 ) 2 − f ( 0 ) + 1 ?
Log in to reply
They just substituted f(0) in for x.
f ( x ) = x 2 − x + 1 ⟹ f ( f ( 0 ) ) = f ( 0 ) 2 − f ( 0 ) + 1
Log in to reply
f ( f ( x ) ) = x 2 − x + 1 = f ( x )
Did you substitute x = f ( 0 ) ? Then the LHS should be f ( f ( f ( 0 ) ) ) instead of f ( f ( 0 ) ) .
Can u please explain the statement "but f(0) Can not be 0 ,otherwise there will be divergence in the mapping of the function" .
You are wrong
Now we put f(x)=y, and we have that y∈R. Hence, we can write f(f(y))=y^2-y+1, but f(y)=f(f(x))=x^2-x+1 So we get f(x^2-x+1)=〖f(x)〗^2-f(x)+1 Now f(1)=〖f(1)〗^2-f(1)+1 by setting x=1 yielding f(1)=1 And set x=0 gets f(0)=0 or f(0)=1, but if f(0)=0 then f(f(0))=f(0)=1 contradiction.
Your solution is not valid.
Yes, it's true that the answer holds for f ( x ) = x , actually it's true for any y , where f ( x ) = y , but you need to prove it first.
Wwrroonngg solution
f ( x ) = a x 2 + b x + c
f ( f ( x ) ) = a ( a x 2 + b x + c ) + b ( a x 2 + b x + c ) + c
f ( f ( x ) ) = ( a 2 + a b ) x 2 + ( a b + b 2 ) x + a c + b c + c
We know that f ( f ( x ) ) = x 2 − x + 1 so then we should have:
a 2 + a b = 1 = > a ( a + b ) = 1
a b + b 2 = − 1 = > b ( a + b ) = − 1
a c + b c + c = 1 = > c ( a + b + 1 ) = 1
From the first two we will have a = -b
Using this in the third we will have c = 1
f ( x ) = a x 2 − a x + 1
f ( 0 ) = 1
f(f(x)) = x 2 - x - 1 Here, if we take the inner f(x)= a,
f(a) = 1
So, a = f(x) = 1 , no matter what the value of x is, f(x) will always be 1. You could think of it as a graph of x versus y where y = f(x) = 1, hence a line parallel to the x axis as y = 1.
Here, since x = 0, f(x) = 1
(even when x= .....-5,-4,-3,-2,-1,0,1,2,3,4,5.... )
in the given equation f(f(x)) first replace x with f(x). u will get f(f(f(x)))=f(x)^2-f(x)+1. after this replace x first with 0 and then with 1 solve the quadratic and then u will get f(0) =1.
by substitution in equation f(x)=0 so f(0)=0^2-0+1=1
Moderator note:
Wrong. You get f ( f ( 0 ) ) = 1 and not f ( 0 ) = 1 .
Are you crazy?
Find the number a that f ( f ( a ) ) = a
f ( f ( a ) ) = a 2 − a + 1 = a
a 2 − 2 a + 1 = 0
( a − 1 ) 2 = 0
a = 1
It means f ( f ( 1 ) ) = 1 , if we put 0 in the composit function f(f(0)) = 1 = f(1)
than f(0) = 1
Easy question for secondary (KS4/5) students.
If I rewrite the function as g(f(x))=x^2 - x + 1. I see that the function is an incomplete square. G(f(x))=x^2 -2x + 1 + x = (x - 1)^2 + x = (x - 1)^2 + (x - 1) + 1. Now I know that f(x)=x - 1. I replace it with y. Now g(y)=y^2 + y + 1. Put y = 0. You get g(y)=1.
f(f(f(0)))=f(1) but also (by assiciativity of function composition) f(f(f(0)))=f(0)^2-f(0)+1 and so f(0)^2-f(0)+1=f(1)
So it's seems worthy to find f(1) first. Employing the same technique we get:
f(1)=f(1)^2-f(1)+1 Which is solved to f(1)=1 thus: f(0)^2-f(0)+1=1 and f(0) is must be 0 or 1.
but if f(0) is 0 then f(f(0))=f(0)=0 and not 1 as it should be.
so f(0)=1
Part of me really does love the cleverness that is required to solve this problem, but I'm slightly disappointed by the fact that the answer is so easy to guess by faulty logic. Obviously, the nature of the parameters makes this aspect difficult to design around, but it still would've been nice.
The function is definitely not a polynomial, but I can't seem to prove it even exists, let alone find an explicit formulation.
I might disagree with you but i cant deny to you .. i found the answer .. but i also tried to find the function itself. . I have not reached the solution but i think i am mid way. Kinda help me. We take the intial function as (X^1/2)^2 + something I am not able to find that something.. please help
first find f(0) f(0)=1 thn f(f(0))=f(1)=1
f(x) = 0-0+1 = 1 , let f(x) = y =1 , f(y) = (1^{2}) -1+1 = 1
We can see that f has its inverted on ( − ∞ , 2 1 ) because suppose there are x , y ∈ ( − ∞ , 2 1 ) , x = y and f ( x ) = f ( y ) , this will lead to 0 = f ( f ( x ) ) − f ( f ( y ) ) = ( x 2 − x + 1 ) − ( y 2 − y + 1 ) = ( x − y ) ( x + y − 1 ) = 0 (contradiction)
We call g the inverted of f . We then have: f ( x ) = g ( f ( f ( x ) ) = g ( x 2 − x + 1 ) and f ( x ) = f ( f ( g ( x ) ) ) = g 2 ( x ) − g ( x ) + 1
With that, we have: f ( 0 ) = g ( 1 ) = g 2 ( 1 ) − g ( 1 ) + 1
We can easily see that f ( 0 ) = g ( 1 ) = 1 in this case
f ( x ) = g ( f ( f ( x ) ) )
This is not necessarily true; remember that g has codomain ( − ∞ , 2 1 ) , so if f ( x ) ≥ 2 1 the statement doesn't hold.
The first paragraph is not true. The function need not be surjective, or injective.
In fact, what you have shown is that if x + y = 1 , then f ( x ) = f ( y ) .
In particular, if we can show that f ( 1 ) = 1 , then f ( 0 ) = f ( 1 ) = 1 .
For x ≤ 2 1 we know that x 2 − x + 1 is invertible. Since ( f ∘ f ) ( x ) = x 2 − x + 1 its clear that f is both injective and surjective and in consecuence inversible, for x ≤ 2 1 . But f need not be inversible. Note that ( f ∘ f ) : ( − ∞ , 2 1 ] ↦ [ 4 3 , + ∞ ) Then f : ( − ∞ , 2 1 ] ↦ A and then will have to be f : A ↦ [ 4 3 , + ∞ ) . This is not posible.
This is the right way (i think)
f ( f ( 0 ) ) = f ( f ( 1 ) ) = 1 by subbing into original equation
f ( 0 ) = f ( 1 )
f ( x ) = c , c is some constant
We get f ( c ) = x 2 − x + 1 = c (remember that f ( x ) is a constant)
This implies that x 2 − x = 0 = > x = 0 , x = 1 and c = 1
f ( 0 ) = c = 1
Moderator note:
As pointed out, It is not true that f ( x ) is a constant c for all x .
However, what is true is that for c = f ( 0 ) = f ( 1 ) , we have f ( c ) = c .
We can say for any a , b , that f ( a ) = f ( b ) ⟹ a = b if and only if we know that f ( x ) is an injective function, however we are not told that f ( x ) is an injective function. Therefore it will not be correct to conclude f ( 0 ) = f ( 1 ) from f ( f ( 0 ) ) = f ( f ( 1 ) ) .
For example, let h ( x ) = x 2 − 1 which is not injective. We can see that h ( h ( 0 ) ) = h ( h ( 2 ) ) = 1 . However, that does not imply that h ( 0 ) = h ( 2 ) . In fact, h ( 0 ) = − 1 and h ( 2 ) = 1 and they are not equal.
Are you saying that f ( x ) is a constant function ?
Log in to reply
From f ( 0 ) = f ( 1 ) , yes
Log in to reply
It would be incorrect to make such a conclusion.
Consider a function g ( x ) = x ( x − 1 ) . We see that g ( 0 ) = g ( 1 ) , but g ( x ) is not a constant function.
Also, if f ( x ) is a constant function, then f ( f ( x ) ) is also a constant function, i.e. independent of x . However we see that f ( f ( x ) ) depends on x .
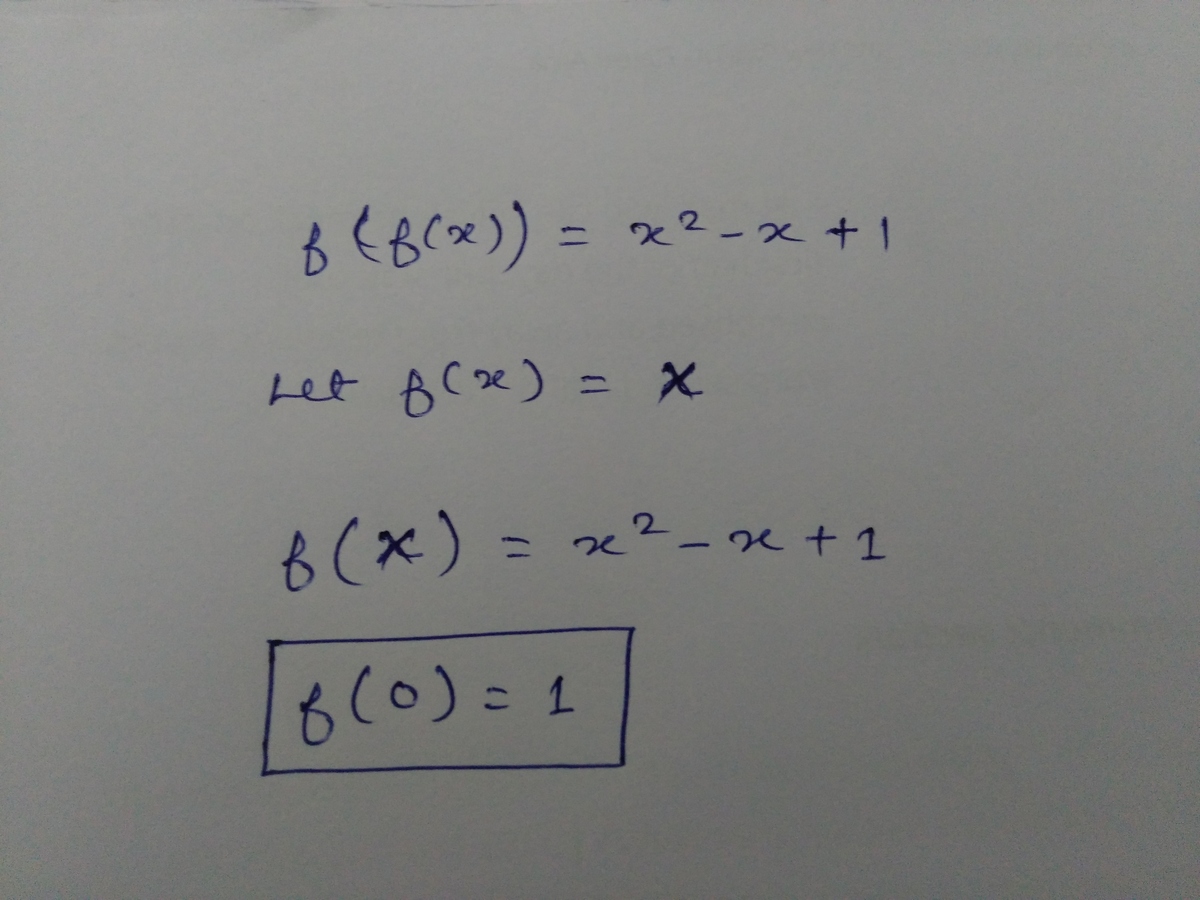
Let P ( x ) be the statement f ( f ( x ) ) = x 2 − x + 1 .
First, we will find the value of f ( 1 ) . Suppose f ( 1 ) = a . From P ( 1 ) , we have
f ( a ) = f ( f ( 1 ) ) = 1 2 − 1 + 1 = 1
From P ( a ) , we have
f ( f ( a ) ) f ( 1 ) a 0 0 a = a 2 − a + 1 = a 2 − a + 1 = a 2 − a + 1 = a 2 − 2 a + 1 = ( a − 1 ) 2 = 1
Thus f ( 1 ) = a = 1 .
Now we move to f ( 0 ) . Suppose f ( 0 ) = b . Then, from P ( 0 ) , we have
f ( b ) = f ( f ( 0 ) ) = 0 2 − 0 + 1 = 1
From P ( b ) , we have
f ( f ( b ) ) f ( 1 ) 1 0 0 = b 2 − b + 1 = b 2 − b + 1 = b 2 − b + 1 = b 2 − b = b ( b − 1 )
Thus, b = 0 or b = 1 . However, if b = 0 , then we have f ( 0 ) = 0 , so f ( f ( 0 ) ) = f ( 0 ) = 0 , contradicting P ( 0 ) stating that f ( f ( 0 ) ) = 1 . Thus f ( 0 ) = b = 1 , which we can verify to work.
This solution is actually incomplete: it hasn't been proven that f exists, only that f ( 0 ) = 1 for any satisfying f .