Fractional Equation!
Find the number of solutions to
⟨ x 2 ⟩ = ⟨ x ⟩ in the range [ 1 , 7 ] .
Here, ⟨ n ⟩ denotes the fractional part of x : ⟨ 3 . 4 ⟩ = 0 . 4
The answer is 43.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Incorrect; f ( x ) = x 2 − x takes every real value in [ 0 , 4 2 ] , not 4 9 . Thus the answer is 4 3 , not 5 0 .
Edit: Solution and answer edited, so this no longer holds.
Log in to reply
You are correct, my mistake.
even I gave 43 and it was shown incorrect Please rectify the problem
Log in to reply
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the “dot dot dot” menu in the lower right corner. This will notify the problem creator who can fix it the issues.

Did the same!
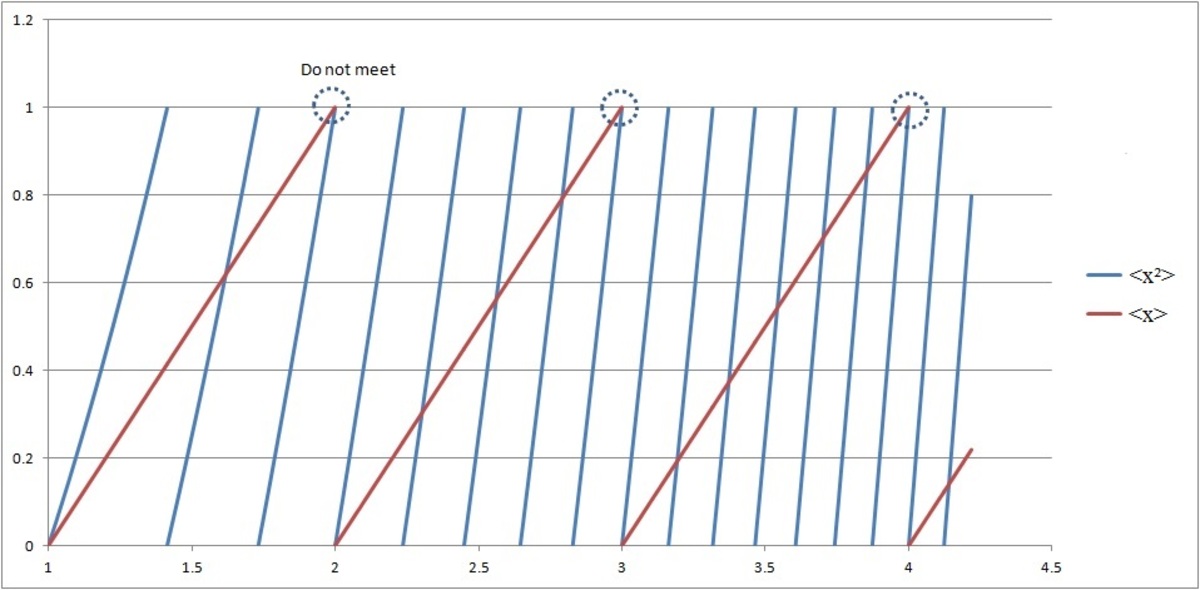
It can be seen that 0 ≤ ⟨ x 2 ⟩ < 1 when n ≤ x < n + 1 , where n = 1 , 2 , 3 , . . . 7 and that 0 ≤ ⟨ x ⟩ < 1 when n ≤ x < n + 1 . For x ∈ [ 1 , 7 ] , there are 4 8 ranges of ⟨ x 2 ⟩ ∈ [ 0 , 1 ) and 6 ranges of ⟨ x ⟩ ∈ [ 0 , 1 ) . The graph above shows the curves of ⟨ x 2 ⟩ ∈ [ 0 . 1 ) and ⟨ x ⟩ ∈ [ 0 . 1 ) . We see that from x ∈ [ 1 , 2 ) , ⟨ x 2 ⟩ ∈ [ 0 . 1 ) and ⟨ x ⟩ ∈ [ 0 . 1 ) meet at x = 1 and x ∈ ( 2 , 3 ) , and they do not meet in x ∈ ( 3 , 2 ) as marked by the dash-line circle. Similarly, they do not meet in x ∈ ( 8 , 3 ) , ∈ ( 1 5 , 4 ) , ∈ ( 2 4 , 5 ) , ∈ ( 3 5 , 6 ) and ∈ ( 4 8 , 7 ) .
Therefore, the number of solutions or the points ⟨ x 2 ⟩ and ⟨ x ⟩ meet = 4 8 − 6 + 1 = 4 3 .
Consider the function f ( x ) = x 2 − x . Note that the function is strictly increasing and continuous for x > 1 .
If ⟨ x 2 ⟩ = ⟨ x ⟩ , we must have x 2 − x = n for some integer n . In the range [ 1 , 7 ] , f(x) takes on every real value in [ 0 , 4 2 ] . It is also strictly increasing, so it takes on every real value in [ 0 , 4 2 ] exactly once.
Because there are 43 integers in [ 0 , 4 2 ] , there are 43 values of x for which x 2 − x = n , meaning that there are 4 3 values of x such that ⟨ x 2 ⟩ = ⟨ x ⟩ .
As a bonus, solving the quadratic with the quadratic formula gives the values of x as x = 2 1 ± 1 + 4 n for n in the range [ 0 , 4 2 ]