An algebra problem by Martin Nikolov
Evaluate : 4 + 7 − 4 − 7 − 2
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
how did u get that 3rd step
Log in to reply
By making Perfect Square
ur is wrong
First let S = 4 + 7 − 4 − 7 , so S 2 = 4 + 7 + 4 − 7 − 2 4 2 − 7 = 2 . Therefore, S = 2 , so the total sum is 2 − 2 = 0
Luv your solution
4 + 7 = 2 7 + 2 1 + 2 . 2 . 2 7 . 1
given expression
= ( 2 7 + 2 1 ) 2 − ( 2 7 − 2 1 ) 2 − 2
= 2 2 − 2
x= √(4+√(7)) - √(4-√(7)) - √(2) ⇒
( x+√(2))² = ( √(4+√(7)) - √4-√7)) )² ⇒
x²+2√(2)x+2=4+√ (7)-2√(16-7) +4-√(7) ⇒
x²+2√(2)x+2 -2=4-2√(9)+4 -2
x²+2√(2)x = 6 - 2(±3)
1.) x² +2√(2)x = 6-(6)
2.) x² + 2√(2)x = 6+(6)
1.) x = -2√(2) or 0
*
*
2.) x = -(2)± √(14)
I got four solutions but I pick the only integer I got. sorry for the weird confusions.
\sqrt(4+\sqrt(7))-\sqrt(4-\sqrt(7))-\sqrt(2) =(\frac{1}{\sqrt(2)})\times \sqrt(7 +2times (\sqrt(7))+1)-\sqrt(7+1-2times (\sqrt(7)))-2
ans = 0 sqrt(4+sqrt(7)) = (sqrt(7) + 1)/sqrt(2) sqrt( 4 - sqrt(7) ) = (sqrt(7) - 1)/sqrt(2) sqrt( 4 + sqrt(7) ) - sqrt( 4 - sqrt(7) ) = sqrt(2) sqrt(2) - sqrt(2) = 0
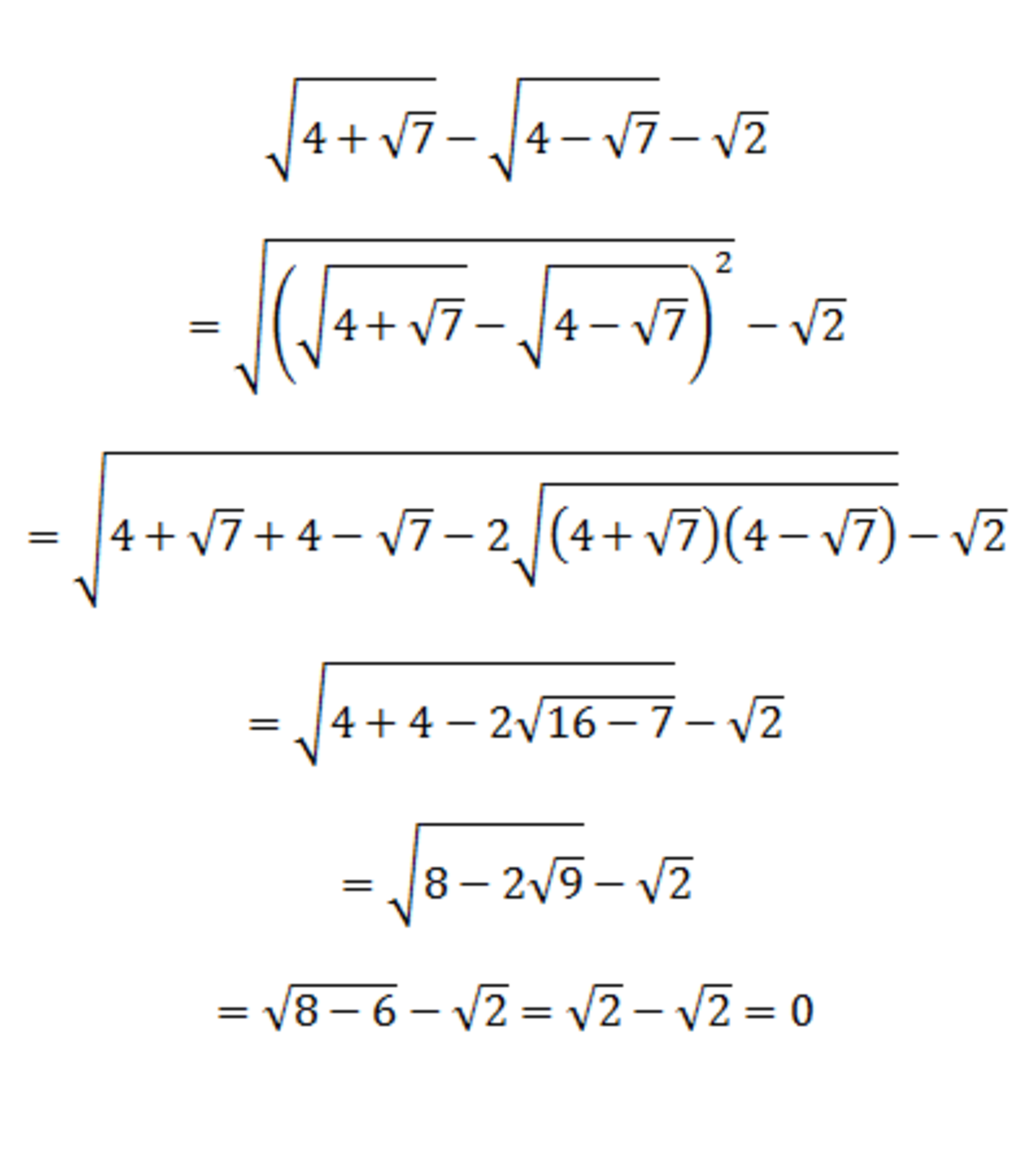
4 + 7 − 4 − 7 − 2
= 2 1 ( 8 + 2 7 − 8 − 2 7 − 2 )
= 2 1 [ ( 7 + 1 ) − ( 7 − 1 ) − 2 ] = 0