An algebra problem by Martin Nikolov

Squaring both sides of $ab = a - b \quad \Rightarrow a^2b^2 = a^2 - 2ab + b^2$

Dividing both sides with $ab \quad \Rightarrow ab = \dfrac {a}{b} - 2 + \dfrac {b} {a}$

Rearranging, we have $\dfrac {a}{b} + \dfrac {b} {a} - ab = \boxed {2}$

$\dfrac{a}{b}+\dfrac{b}{a}-ab = \left(\dfrac{a}{b}-a\right)+\left(\dfrac{b}{a}+b\right) = \dfrac{a-ab}{b}+\dfrac{b+ab}{a}$

$= \dfrac{a-(a-b)}{b}+\dfrac{b+(a-b)}{a} = \dfrac{b}{b}+\dfrac{a}{a} = 1+1 = \boxed{2}$

Solve for a 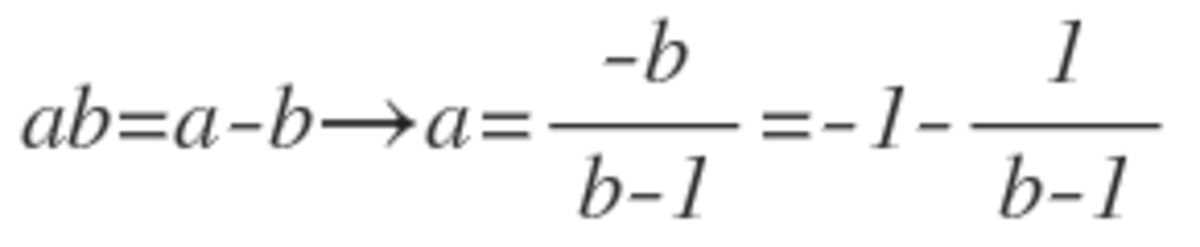We equate equation with any number. For example b = 3 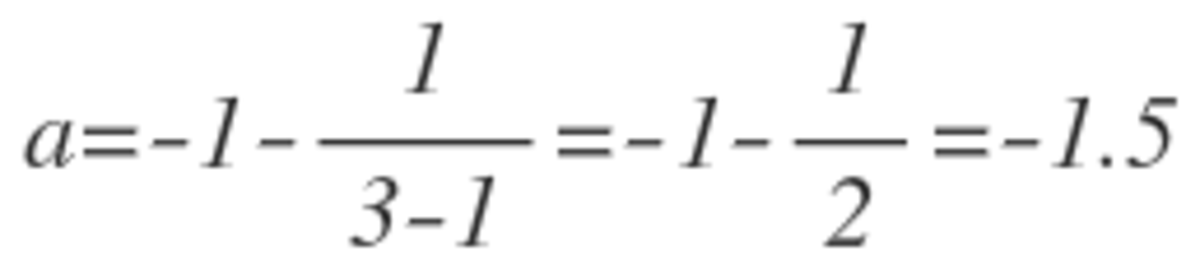Now we have two values a = -1.5 and b = 3. Solve for in the last formula

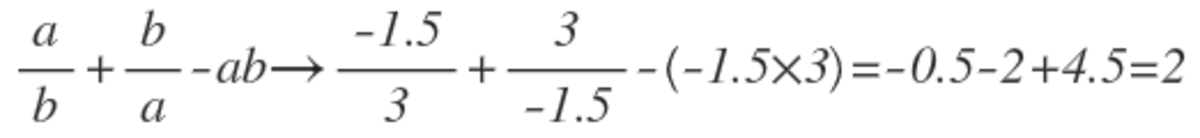
Pd. I'm 15 years old

a/b+b/a - ab=a^2+b^2/ab - ab

We can write a^2+b^2 /ab - ab as (a-b)^2+2ab/ab - ab

But given a-b=ab

By substituting a-b=ab in (a-b)^2+2ab/ab - ab

We get a^2.b^2 + 2ab/ab - ab

=a^2.b^2 + 2ab - a^2.b^2 / ab

=2ab/ab

=2

ab=a-b ==> a=-2 ; b=2 now put in a/b +b/a-ab ==> -1-1+4 = 2

We get by squaring both sides in the given information:

$\displaystyle ab = a-b \Rightarrow a^{2}b^{2} = (a-b)^2 \Rightarrow a^{2}b^{2} = a^{2} + b^{2} - 2ab$

Dividing both sides by ab , we get:

$\displaystyle ab = \frac{a}{b} + \frac{b}{a} - 2 \Rightarrow \frac{a}{b} + \frac{b}{a} - ab = \boxed{2}$

And hence the answer!

a/b+b/a=(a^2+b^2)/ab Now ,(ab)^2=(a-b)^2 So, (a^2+b^2-a^2-b^2+2ab)/ab So, 2ab/ab=2