painting a house
Andy and Ben can paint a house in ten days; Andy and Chris can do it in twelve days; Ben and Chris can do it in twenty days. How many days will Chris take to do the work alone?
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
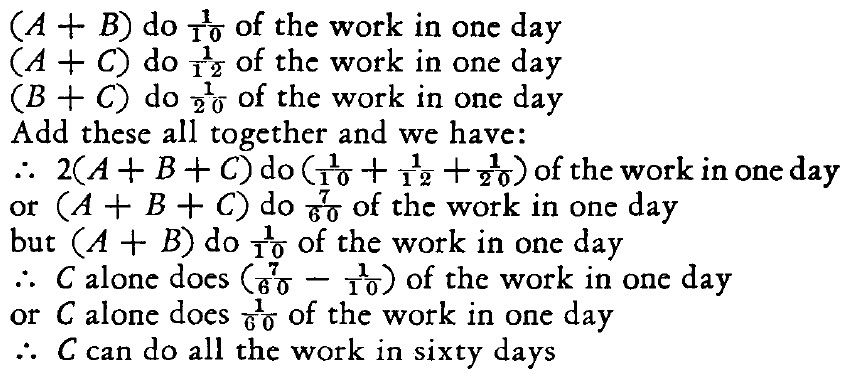
Here is another good problem that you may try. https://brilliant.org/problems/who-gets-the-buck-2/ It has been qualified for level 2 algebra but the no. of solvers required is yet not met.
Andy can finish the work in A days. Ben can finish the work in B days. Chris can finish the work in C days.
In one day, Andy can finish A 1 work. Similar for Ben and Chris. Given,
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ A 1 + B 1 A 1 + C 1 B 1 + C 1 = 1 0 1 . . . ( 1 ) = 1 2 1 . . . ( 2 ) = 2 0 1 . . . ( 3 )
In one day, Andy and Ben can finish 1 0 1 work, together. And similar for Ben & Chris, and Andy & Chris.
( 1 ) + ( 2 ) + ( 3 ) gives
A 1 + B 1 + C 1 = 6 0 7 . . . ( 4 ) .
( 4 ) − ( 1 ) gives
C 1 = 6 0 1
Hence, the answer is C = 6 0 .
That is the exact same way I did it
Let the work be W and the rates of doing work of A , B and C be a , b and c respectively. Then we have:
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ 1 0 ( a + b ) = W 1 2 ( c + a ) = W 1 0 ( a + b ) = W ⟹ a + b = 1 0 W ⟹ c + a = 1 2 W ⟹ b + c = 2 0 W . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
( 3 ) + ( 2 ) − ( 1 ) : 2 c 6 0 c = 2 0 W + 1 2 W − 1 0 W = W ( 6 0 3 + 5 − 6 ) = W
It will take C 6 0 days to do the work alone.
Let's do it without Algebra. Let Andy be A, Ben be B and Chris be C.
Let's suppose total area to be painted is 60 units. (LCM of 10, 12 and 20)
A+B can paint 6 units per day
A+C can paint 5 units per day
B+C can paint 3 units per day
From first and second statement we see that B can paint one more unit than C in one day. When we look at the third statement it is obvious that C paints 1 unit per day, B paints 2 units per day. It can be further confirmed that A paints 4 units per day though that is not needed for our solution. So C will need 60 days.