Multiple perfect squares
Do there exist 3 distinct positive integers ( x , y , z ) such that x + y , y + z , z + x , and x + y + z are all perfect squares?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
We are looking for distinct positive integers a , b , c , d with a 2 + b 2 + c 2 = 2 d 2 and a , b , c < d . If we define α = d a , β = d b , γ = d c , then α , β , γ are rationals with 0 < α , β , γ < 1 and α 2 + β 2 + γ 2 = 2 .
Define u , v ∈ Q by the formulae α = 1 − u γ , β = 1 − v γ , Then ( 1 − u γ ) 2 + ( 1 − b γ ) 2 + γ 2 γ [ ( u 2 + v 2 + 1 ) γ − 2 ( u + v ) ] = 2 = 0 so that γ = u 2 + v 2 + 1 2 ( u + v ) Since γ > 0 and α , β < 1 we deduce that u , v > 0 . Since γ < 1 we deduce that 2 ( u + v ) < u 2 + v 2 + 1 , and hence that ( u − 1 ) 2 + ( v − 1 ) 2 > 1 . If u , v < 1 it is clear that α = 1 − u γ > 1 − u > 0 β = 1 − v γ > 1 − v > 0 Thus we obtain suitable values of α , β , γ , from which we can retrieve suitable values of a , b , c , d , by choosing (nearly) any pair of rationals u , v such that 0 < u < 1 0 < v < 1 ( u − 1 ) 2 + ( v − 1 ) 2 > 1 This is the region in the u v -plane defined by the circle centre ( 1 , 1 ) and radius 1 , the u -axis and the v -axis.
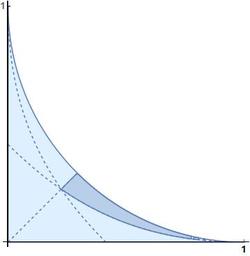 If we choose
u
=
v
, then
α
=
β
. The conditions for
γ
to be distinct from
α
,
β
are more complex:
(
u
+
v
+
1
)
2
=
2
(
u
2
+
1
)
(
u
+
v
+
1
)
2
=
2
(
v
2
+
1
)
but it is easy enough to choose
u
,
v
in the above region which satisfy these extra conditions. Indeed, if we pick
u
,
v
in the darker shaded region, we always obtain
0
<
α
<
β
<
γ
<
1
. The other five regions give the other possible orderings of
α
,
β
,
γ
.
If we choose
u
=
v
, then
α
=
β
. The conditions for
γ
to be distinct from
α
,
β
are more complex:
(
u
+
v
+
1
)
2
=
2
(
u
2
+
1
)
(
u
+
v
+
1
)
2
=
2
(
v
2
+
1
)
but it is easy enough to choose
u
,
v
in the above region which satisfy these extra conditions. Indeed, if we pick
u
,
v
in the darker shaded region, we always obtain
0
<
α
<
β
<
γ
<
1
. The other five regions give the other possible orderings of
α
,
β
,
γ
.
For example, with u = 3 1 , v = 2 1 4 we obtain α = 2 3 1 6 β = 2 3 1 9 γ = 2 3 2 1 and hence we can retrieve a = 1 6 , b = 1 9 , c = 2 1 and d = 2 3 .
Irritatingly, having done all the hard work to parametrize the solutions of the equation, I got the conditions on u , v wrong initially, and made the wrong solution choice!
Log in to reply
Very nice! You have effectively parametrized all possible solutions to the problem. (I fixed one typo in the first line of the first display equation. )
Very nice way to parametrize and find the general solution! If we take u = 1/4 and v = 1/5, then we recover the solution I found a = 39, b = 41 and c = 40.
This is the best solution so far! I wished someone could parametrize the solutions. Unless I got it wrong, why doesn't every pair of u , v give suitable values for the equation? Moreover, can we add some conditions on u , v so that x , y , z are positive?
Log in to reply
The conditions that a , b , c , d are nonzero, distinct, positive, with a , b , c < d , ensure that x , y , z are nonzero, distinct and positive.
There are conditions on u , v to ensure that α , β , γ are distinct and lie in ( 0 , 1 ) . That is why u , v must be distinct and lie in the region defined by the circle and the axes. However, almost any pair of distinct rational u , v in that region will give a viable solution.
Nice! There is only one thing I gon't get: why are u,v<1? In other words, are there solutions where 1<u<2?
Log in to reply
The actual conditions for α and β to be positive are complicated, but they restrict the solutions to the region I have indicated.
"Also, if is a solution without a square as common factor, then two of the numbers are multiples of four, and the other is one more than a multiple of four. Of the perfect squares, one is even and the other three are odd." How do you know this man?
Log in to reply
It appears that I may have mistyped something here-- but let me explain.
If a 2 , b 2 , c 2 are all even, then they have a common factor 2 2 . We rule out this situation, and may therefore assume that one of the number is odd--say, a 2 . But the sum 2 d 2 is even, so that there must be precisely one other odd number--say, b 2 . Thus we get a 2 + b 2 + c 2 = odd + odd + even = 2 d 2 . Now the square of an odd number is one more than a multiple of four: ( 2 x + 1 ) 2 = 4 ( x 2 + k ) + 1 ; and the square of an even number is a multiple of four. Therefore a 2 + b 2 = ( 4 k + 1 ) + ( 4 k ′ + 1 ) + k ′ ′ = 4 ( k + k ′ + k ′ ′ ) + 2 = 2 [ 2 ( k + k ′ + k ′ ′ ) + 1 ] = 2 d 2 , which proves that d 2 (and therefore d ) must be odd. Thus we have a 2 + b 2 + c 2 = odd + odd + even = 2 odd ; or a 2 + b 2 + c 2 ≡ 1 + 1 + 0 ≡ 2 ⋅ 1 ≡ 2 d 2 mod 4 .
Even I got the equation. After that how do we find the solution without a computer / lots of trial and error.
How do you find the solution?
Note: It is better to explain that "Let x + y + z = d 2 , y + z = a 2 hence x = d 2 − a 2 ". instead of making it seem magical that " x = ( d − a ) ( d + 1 ) .
We are looking for distinct positive integers a , b , c , d with a 2 + b 2 + c 2 = 2 d 2 and a , b , c < d . If we define α = d a , β = d b , γ = d c , then α , β , γ are rationals with 0 < α , β , γ < 1 and α 2 + β 2 + γ 2 = 2 .
Define u , v ∈ Q by the formulae α = 1 − u γ , β = 1 − v γ , Then ( 1 − u γ ) 2 + ( 1 − b γ ) 2 + γ 2 γ [ ( u 2 + v 2 + 1 ) γ − 2 ( u + v ) ] = 2 = 0 so that γ = u 2 + v 2 + 1 2 ( u + v ) Since γ > 0 and α , β < 1 we deduce that u , v > 0 . Since γ < 1 we deduce that 2 ( u + v ) < u 2 + v 2 + 1 , and hence that ( u − 1 ) 2 + ( v − 1 ) 2 > 1 . If u , v < 1 it is clear that α = 1 − u γ > 1 − u > 0 β = 1 − v γ > 1 − v > 0 Thus we obtain suitable values of α , β , γ , from which we can retrieve suitable values of a , b , c , d , by choosing (nearly) any pair of rationals u , v such that 0 < u < 1 0 < v < 1 ( u − 1 ) 2 + ( v − 1 ) 2 > 1 This is the region in the u v -plane defined by the circle centre ( 1 , 1 ) and radius 1 , the u -axis and the v -axis.
 If we choose
u
=
v
, then
α
=
β
. The conditions for
γ
to be distinct from
α
,
β
are more complex:
(
u
+
v
+
1
)
2
=
2
(
u
2
+
1
)
(
u
+
v
+
1
)
2
=
2
(
v
2
+
1
)
but it is easy enough to choose
u
,
v
in the above region which satisfy these extra conditions. Indeed, if we pick
u
,
v
in the darker shaded region, we always obtain
0
<
α
<
β
<
γ
<
1
. The other five regions give the other possible orderings of
α
,
β
,
γ
.
If we choose
u
=
v
, then
α
=
β
. The conditions for
γ
to be distinct from
α
,
β
are more complex:
(
u
+
v
+
1
)
2
=
2
(
u
2
+
1
)
(
u
+
v
+
1
)
2
=
2
(
v
2
+
1
)
but it is easy enough to choose
u
,
v
in the above region which satisfy these extra conditions. Indeed, if we pick
u
,
v
in the darker shaded region, we always obtain
0
<
α
<
β
<
γ
<
1
. The other five regions give the other possible orderings of
α
,
β
,
γ
.
For example, with u = 3 1 , v = 2 1 4 we obtain α = 2 3 1 6 β = 2 3 1 9 γ = 2 3 2 1 and hence we can retrieve a = 1 6 , b = 1 9 , c = 2 1 and d = 2 3 .
Irritatingly, having done all the hard work to parametrize the solutions of the equation, I got the conditions on u , v wrong initially, and made the wrong solution choice!
@Mark Hennings , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.
@Mark Hennings Really nice solution. I don't understand how have you got the conditions for γ = α and γ = β . For instance γ = α , I have tried to substitute and i've got: 1 − u ⋅ u 2 + v 2 + 1 2 ( u + v ) = u 2 + v 2 + 1 2 ( u + v )
but i have obtained a different condition
Log in to reply
Start with your condition and simplify... α 1 − u γ ( 1 + u ) γ 2 ( 1 + u ) ( u + v ) 2 u 2 + 2 u v + 2 u + 2 v ( u + v + 1 ) 2 = u 2 + v 2 + 1 + 2 u v + 2 u + 2 v = γ = γ = 1 = u 2 + v 2 + 1 = u 2 + v 2 + 1 = ( u 2 + v 2 + 1 ) + ( v 2 − u 2 + 1 ) = 2 ( v 2 + 1 ) and similarly for the other condition.
Diophantus of Alexandria set out a pattern for solving such problems - start out hopefully, see where the maths goes, and be perfectly content if it leads you to an answer! In this spirit let us call the three numbers we are looking for a,b and c and start with the observation that for any integer x, the three equations -
a + b + c = ( x + 1 ) 2 … 1 a + b = x 2 … 2 b + c = ( x − 1 ) 2 … 3
guarantee that three of the conditions are automatically satisfied, and so the next step is to find x so that a + c is also a square. Well, taking 2 × 1 − 2 − 3 gives
a + c = 2 ( x + 1 ) 2 − x 2 − ( x − 1 ) 2 = 6 x + 1
So all we need to do is to find x, so that 6 x + 1 is a square. There are an infinite number of possible values for x which make 6 x + 1 square, but to meet the full requirements of this problem we must check retrospectively that the integers a,b and c are indeed positive and distinct. For instance x = 2 0 will do because 6 x + 1 = 1 2 1 which is a square, and then substituting x = 2 0 into our three numbered equations gives
a + b + c = 4 4 1 a + b = 4 0 0 b + c = 3 6 1
which are easily solved to give distinct positive integers
a = 8 0 b = 3 2 0 c = 4 1
which satisfy all the conditions of the problem.
One solution is x = 720, y = 801 and z = 880. We can check that 720 + 801 = 39^2, 801 + 880 = 41^2, 880 + 720=40^2 and 720 + 801 + 880 = 49^2.
Note that ⎩ ⎪ ⎨ ⎪ ⎧ x = 7 2 0 = 8 ⋅ 9 0 y = 8 0 1 = 9 ⋅ 8 9 z = 8 8 0 = 1 0 ⋅ 8 8 8 + 9 0 = 9 8 9 + 8 9 = 9 8 1 0 + 8 8 = 9 8 ; and we recover the perfect squares 3 9 2 , 4 0 2 , 4 1 2 , 4 9 2 by observing that ⎩ ⎪ ⎨ ⎪ ⎧ 8 = 4 9 − 4 1 9 = 4 9 − 4 0 1 0 = 4 9 − 3 9 9 0 = 4 9 + 4 1 8 9 = 4 9 + 4 0 8 8 = 4 9 + 3 9 . There is some serious elegance going on here!
Log in to reply
Yeah, it's quite an interesting problem, I wonder if there is a general solution to this. Even for primitive solutions, there are infinite number of them. By primitive I mean x, y, z don't share common factors.
We can generate infinite number of primitive solutions by using solution of the Pell equation d^2 - 6k^2 = 1 and a = 2k-1, b = 2k + 1, c = 2k, as I discussed below. But this does not include the primitive solution you found, which is a = 16, b = 19, c = 21 and d = 23. So the question of whether a general solution exists is still out there.
ya how is it
Nice problem. I used it as an inspiration. If you want to think more about it visit my problem.
Hey, thanks for posting. Just out of curiosity, how did you find it?
Log in to reply
Nice problem. Let x + y = a^2, y + z = b^2, z + x = c^2, x + y + z= d^2, so we need a^2 + b^2 + c^2 = 2 d^2. Then I just tried for a = 2k-1, b = 2k + 1, c = 2k, which gives d^2 - 6 k^2 = 1. This is Pell's equation with n = 6, with the second smallest solution being d = 49, k = 20. From that we get a = 39, b = 41 and c = 40. Then it's easy to solve x = 720, y = 801 and z = 880.
As all that is needed to prove that a solution exists, is to find one example, it seems quickest to just start looking for one. Wrote a Python script in about 2 mins, just guessing a solution exists with x , y , z < 1 0 0 0 :
from math import sqrt
def is_square(x, eps=1e-9):
root = sqrt(x)
return abs(int(root) - root) < eps
n = 1000
for x in range(1, n-2):
for y in range(x+1, n-1):
for z in range(y+1, n):
if is_square(x+y) and is_square(y+z) and is_square(x+z) and is_square(x+y+z):
print(x, y, z)
x^2 +y^2 + z^2 is the equation of an solid egg-like structure. Consider an intersecting plane such that 3^2 + 4^2 = 5^2 where x = 3 and y = 4. This is the perfect 3, 4, 5 triangle. Now, rotate the triangle about the long side (z or 5). You will generate a 3-D geometric shape (an egg) which always satisfies the 3,4, 5 ratio now matter how you cut it.
The question is, does there exists positive and distinct x, y, z such that x + y = a^2 , y + z = b^2 , x + z = c^2 and x + y + z = d^2 where a,b,c and d are integers. Solve this linear system to obtain that x = d^2 - b^2,
y = a^2 - d^2 + b^2, z = d^2 - a^2 provided that a^2 + b^2 + c^2 = 2d^2. Note that
(11^2) + (19^2) + (20^2) = 2(21^2) so our restrictions are satisfied if a = 11 , b = 19 ,
c = 20 and d = 21. From this we obtain x = 80 , y = 41 , and z = 320. To verify, we see that
x + y = 121, y + z = 361, x + z = 400, and
x + y + z = 441.
Note that if there is one solution, there are infinitely many; for if ( x , y , z ) is a solution, so is ( n 2 x , n 2 y , n 2 z ) for positive integers n .
Also, if ( x , y , z ) is a solution without a square as common factor, then two of the numbers are multiples of four, and the other is one more than a multiple of four. Of the perfect squares, one is even and the other three are odd.
If we can find four distinct squares a 2 < b 2 < c 2 < d 2 such that a 2 + b 2 + c 2 = 2 d 2 , then a solution is x = ( d − a ) ( d + a ) , y = ( d − b ) ( d + b ) , z = ( d − c ) ( d + c ) .
I found 1 6 2 + 1 9 2 + 2 1 2 = 2 ⋅ 2 3 2 , leading to the choices x = 7 ⋅ 3 9 = 2 7 3 ; y = 4 ⋅ 4 2 = 1 6 8 ; z = 2 ⋅ 4 4 = 8 8 . Then x + y = 2 7 3 + 1 6 8 = 4 4 1 = 2 1 2 ; y + z = 1 6 8 + 8 8 = 2 5 6 = 1 6 2 ; z + x = 8 8 + 2 7 3 = 3 6 1 = 1 9 2 ; x + y + z = 2 7 3 + 1 6 8 + 8 8 = 7 2 9 = 2 3 2 .