We must go deeper
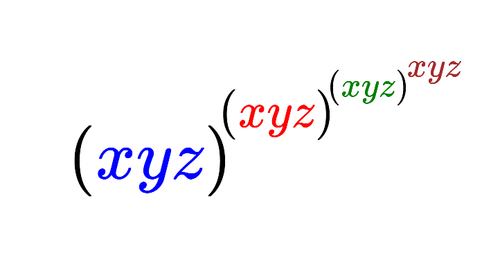 Given that
x
,
y
,
z
are positive real numbers that satisfy the equations:
x
=
y
z
,
y
=
z
x
,
z
=
x
y
, find the value of the expression above.
Given that
x
,
y
,
z
are positive real numbers that satisfy the equations:
x
=
y
z
,
y
=
z
x
,
z
=
x
y
, find the value of the expression above.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
x=y^z => log x = zlogy Similarly, log y = x log z And, log z = y log x
Multiplying above 3 log eqns -> (log x)(log y)(log z) = xyz (logx)(log y)(log z) So, xyz = 1; And hence answer is 1
We claim that x y z = 1 .
Suppose some of x , y , z is equal to 1 ; without loss of generality , suppose x = 1 . Then z = x y implies z = 1 , and y = z x implies that y = 1 . This gives x y z = 1 .
Otherwise, from x = y z and y = z x , we get x = ( z x ) z = z x z . Together with z = x y , we get x = ( x y ) x z = x x y z . Since x > 0 and x = 1 , we can apply logarithm of base x to both sides, giving lo g x x = lo g x x x y z or 1 = x y z .
Thus the expression reduces to 1 1 1 1 = 1 .
y = z x ; having z = x y y = ( x y ) x y = x x y ; having x = y z y = ( y z ) x y y 1 = y x y z The bases are equal and so the exponents are also equal: 1 = x y z Having that we can find that the value of the expression is: 1 1 1 1 = 1
(xyz)^(xyz) = x^(xyz) y^(xyz) z^(xyz) =(x^y)^xz (y^z)^xy (z^x)^yz =z^xz x^xy y^yz =(z^x)^z (x^y)^x (y^z)^y =y^z z^x x^y=xyz . So xyz=1.
x^x=1 , lnx^x =ln1 ,x*lnx =0 , lnx=0 , x=1 ( x>0)
The only way for all 3 equations to be satisfied is if x, y, and z are equal to 1. Since 1^1^1^1 is 1, the solution is 1.
Well this is a multiple choice problem, and notice that the first option "1" satisfies the condition if we let x = y = z = 1. Sounds good of a solution to me!
Moderator note:
Your solution has been marked wrong. You have only shown the desired expression equals to 1 because you let x = y = z = 1 but you didn't show that it's the only solution.
we know x=y^z, y=z^x, z=x^y
take x=y^z
=>x=(z^x)^z
=>x=z^xz
=>x=(x^y)^xz
=>x=x^xyz
=>xyz=1
therefore (xyz)^any number=1
because
1^any number=1