An algebra problem by Nguyễn Hữu Khánh
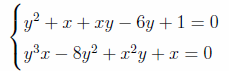 What is the result of
x
+
y
?
What is the result of
x
+
y
?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Exactly, I too did the same, this is really a nice solution to this question. I think this question was made for this observation only!!
From the equation y 2 + x + x y − 6 y + 1 = 0 x = − y 2 + 6 y − 1 ) / ( 1 + y )
Replacing the above value of 'x' in equation y 3 x − 8 y 2 + x 2 y + x = 0 and simplifying, we get an equation completely in y: − y 6 + 6 y 5 − 1 5 y 4 + 2 0 y 3 − 1 5 y 2 + 6 y − 1 = 0
Just by a look at the coefficients (coefficients and constant add up to 0), y =1 is one of the solutions. Replace this value in the first equation to get y = 2. And hence the answer.. 3..
Lazy man's solution:
Equate the two equations and get a 0 on the right side:
y 2 + x + x y − 6 y + 1 = y 3 x − 8 y 2 + x 2 y + x
y 2 + x + x y − 6 y + 1 − y 3 x + 8 y 2 − x 2 y − x = 0
If you just start randomly plugging in values for y (because doing so with x might lead you to need to solve an ugly cubic function), you'll arrive at that of plugging in 1 for y .
1 + x + x − 6 + 1 − x + 8 − x 2 − x = 0
x 2 = 4 → x = ± 2
So the answer ( x + y ) must be either 2 + 1 = 3 or 1 − 2 = − 1 . Try both of them and see that the first of them works.
exactly... :)
Let eq1 be y 2 + x + x y − 6 y + 1 = 0 and eq2 be y 3 x − 8 y 2 − x 2 y + x = 0 .
We begin by multiplying eq 1 by x y and subtract eq 2. With a bit of factoring and rearrangement, we get ( x − 2 ) ( x − 4 ) y 2 = x ( 1 − y ) .
Hence we look at the possibilities when x = 0 , 2 , 4 y = 0 , 1
Here we find the integer solutions (0,0), (2,1), (4,1). By substituting these solutions into the original system of equations, only (2,1) works. Therefore, the answer is 2 + 1 = 3 .
But why should they be integers?
Log in to reply
Because if they weren't, he wouldn't be able to do the factoring that he did.
{ y 2 + x + x y − 6 y + 1 = 0 y 3 x − 8 y 2 + x 2 y + x = 0 ⇒ { ( y 2 + x ) + ( x y + 1 ) − 6 y = 0 ( y 2 + x ) ( x y + 1 ) − 9 y 2 = 0
⇒ { ( y 2 + x ) + ( x y + 1 ) = 6 y ( y 2 + x ) ( x y + 1 ) = 9 y 2 ⇒ { u + v = 6 y u v = 9 y 2 ⇒ { v = 6 y − u u ( 6 y − u ) = 9 y 2
⇒ u 2 − 6 y u + 9 y 2 = ( u − 3 y ) 2 = 0 ⇒ u = 3 y ⇒ y 2 + x = 3 y
⇒ x = 3 y − y 2 ; and substituting in y 2 + x + x y + 1 = 6 y , we have:
y 2 + 3 y − y 2 + ( 3 y − y 2 ) y + 1 − 6 y = − 3 y + 3 y 2 − y 3 + 1 = 0
⇒ y 3 − 3 y 2 + 3 y − 1 = ( y − 1 ) 3 = 0 ⇒ y = 1 ⇒ x = 3 ( 1 ) − 1 2 = 2
⇒ x + y = 2 + 1 = 3