Yet another eight rooks problem
A chessboard is numbered as the figure shows. 8 rooks are placed such that any rook cannot capture another rook. The numbers where the rooks were placed are added up. Considering all the possible accommodations How many distinct sums can be obtained?
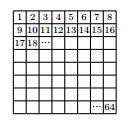
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There is only 1 sum that can be obtained by adding the numbers of the squares on which the rooks are placed anyway for any configuration of 8 rooks that do not attack each other.
Firstly it need to be understood how any configuration of 8 non-attacking rooks should look like such that by considering the possible sums they are conceived according to an organized understanding of the positions of rooks which appear implicitly when thinking of the possible sum , that meaning that when I think of the sums anyway I am thinking also firstly at some positioning of rooks which therefore must be generalized and understood. For this you can observe that any of the 8 rooks when positioned on a square attacks one row and one column therefore meaning that all the 8 rooks will stand on different columns and rows such that they do not attack. Therefore as it is now known that the 8 rooks stand on different rows and columns this means when thinking of either the rows or the columns that for any of the 8 rows/columns there is no rook in the same place as other row.
So now , it's known or rather conceived articulate enough that the 8 rooks should stand for any row/column on square which are not the same number for any 2 different rows/columns.
This speaks about the cumulative number of the squares added as it would intuitively seem to imply that the sum remains constant but is not articulate. In order to see and make articulate how the cumulative sum can vary by the restriction of rooks on different squares for any row/column number organize the rows udner a cumulative criteria. That meaning consider all the squares of the chessboard as being of the form 8 * (q-1) + r-1 where r is the number of the row and q the number of the column. This would lead for example for all squares of the second row to values like 8 * 1 + 1, 8 * 1+2 etc. Now , that an understanding of an organization of the cumulative values has been obtained observe how the cumulative sum varies for different configurations of rooks. Because for any configuration anyway rooks there are always 8 rooks all those rooks will stand on squares which will have all the different values of r and also all the different values for q meaning that all the values of the indices q and r will always add because to anyway the same sum. Another way of expressing this and clarifying it would be to consider firstly that the rooks stand on all the different columns and therefore q will have all values from 1 to 8 meaning that the sum for q obtained is 8 * 7! and afterwards considering the variation for the sum of rows which leads again to 8! meaning therefore that the total constant sum obtained is always 8! + 8 * 7! = 260 anyway.