An algebra problem by Sakanksha Deo
For x 2 + 2 x + 5 to be a factor of x 4 + p x 2 + q , the value of p and q should respectively be:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Another way is to express the degree 4 polynomial as follows:
( x 2 + 2 x + 5 ) ( x 2 + l x + m ) = x 4 + p x 2 + q , for some constants l , m
Expanding the LHS and comparing coefficients of terms from both sides, it can easily be obtained that p = 6 , q = 2 5 .
Can you plz give a detailed solution for this ...plzz.....
Log in to reply
Done that. It is better not to use objective answers if possible. Because, those who answer have only one chance, and it can be wrong because of computation errors, like I frequently do.
let the roots of x 2 + 2 x + 5 be r 1 , r 2 . than the following must also be roots of x 4 + p x 2 + q .it means r 1 4 + p r 1 2 + q = 0 r 2 4 + p r 2 2 + q = 0 adding these 2, ( r 1 4 + r 2 4 ) + p ( r 1 2 + r 2 2 ) + 2 q = 0 by vieta's we have r 1 + r 2 = − 2 , r 1 r 2 = 5 hence r 1 4 + r 2 4 = ( ( r 1 + r 2 ) 2 − 2 r 1 r 2 ) 2 − 2 r 1 2 r 2 2 = − 1 4 r 1 2 + r 2 2 = ( r 1 + r 2 ) 2 − 2 r 1 r 2 = − 6 hence, − 1 4 − 6 p + 2 q = 0 → p = 3 q + 7 the only ones from option satisfying this is 6 , 2 5
The solution can be found using long division as follows: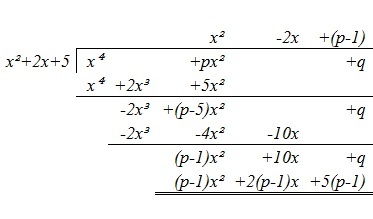
We note that for x 2 + 2 x + 5 to be a factor of x 4 + p x 2 + q ,
{ 2 ( p − 1 ) = 1 0 q = 5 ( p − 1 ) ⇒ p − 1 = 5 ⇒ q = 5 × 5 ⇒ p = 6 ⇒ q = 2 5 ⇒ p , q = 6 , 2 5