This Sum Is That; That Sum Is This
For distinct numbers p and q , consider an arithmetic progression such that
- the sum of the first p terms is equal to q , and
- the sum of the first q terms is equal to p .
What is the sum of the first p + q terms?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
how did you get the first term 'a'?
Log in to reply
First term is always a or a 1 . It's the general form of an AP
Log in to reply
i meant that you didn't show how you get the first term.. (procedure)
Mistake: − d ( p − q ) = 2 p q ( p + q ) ( p − q ) ⟹ − d = p q 2 ( p + q ) , iff p = q , since division by 0 is not allowed.
If p = q we have a counterexample, which you can see from my report.
Total of terms of this progression is : S n = a n + 2 d ∗ ( n 2 − n ) .
We have
S p = q ⟹ a p + 2 d ∗ ( p 2 − p ) = q . . . . . ( 1 ) S q = p ⟹ a q + 2 d ∗ ( q 2 − q ) = p . . . . . ( 2 ) F r o m ( 1 ) a n d ( 2 ) , e l e m i n a t i n g a w e g e t ( q − p ) d = q 2 p − p 2 q = 2 ∗ p q ( p + q ) ∗ ( p − q ) . S i n c e p = q , d p q = − 2 ∗ ( p + q ) . . . . . ( 3 ) A l s o ( 1 ) + ( 2 ) g i v e s S q + S p = q + p = a ( p + q ) + 2 d ∗ ( p 2 + q 2 ) − 2 d ∗ ( p + q ) = p + q . . . . . ( 4 ) S p + q = a ( p + q ) + 2 d ∗ ( p 2 + 2 p q + q 2 ) − 2 d ∗ ( p + q ) = p + q S o f r o m ( 4 ) a n d ( 3 ) , w e g e t , S p + q = a ( p + q ) + 2 d ∗ ( p 2 + q 2 ) − 2 d ∗ ( p + q ) + p q d = p + q + p q d ∴ S p + q = p + q − 2 ( p + q ) = − ( p + q )
This is a very overrated question.
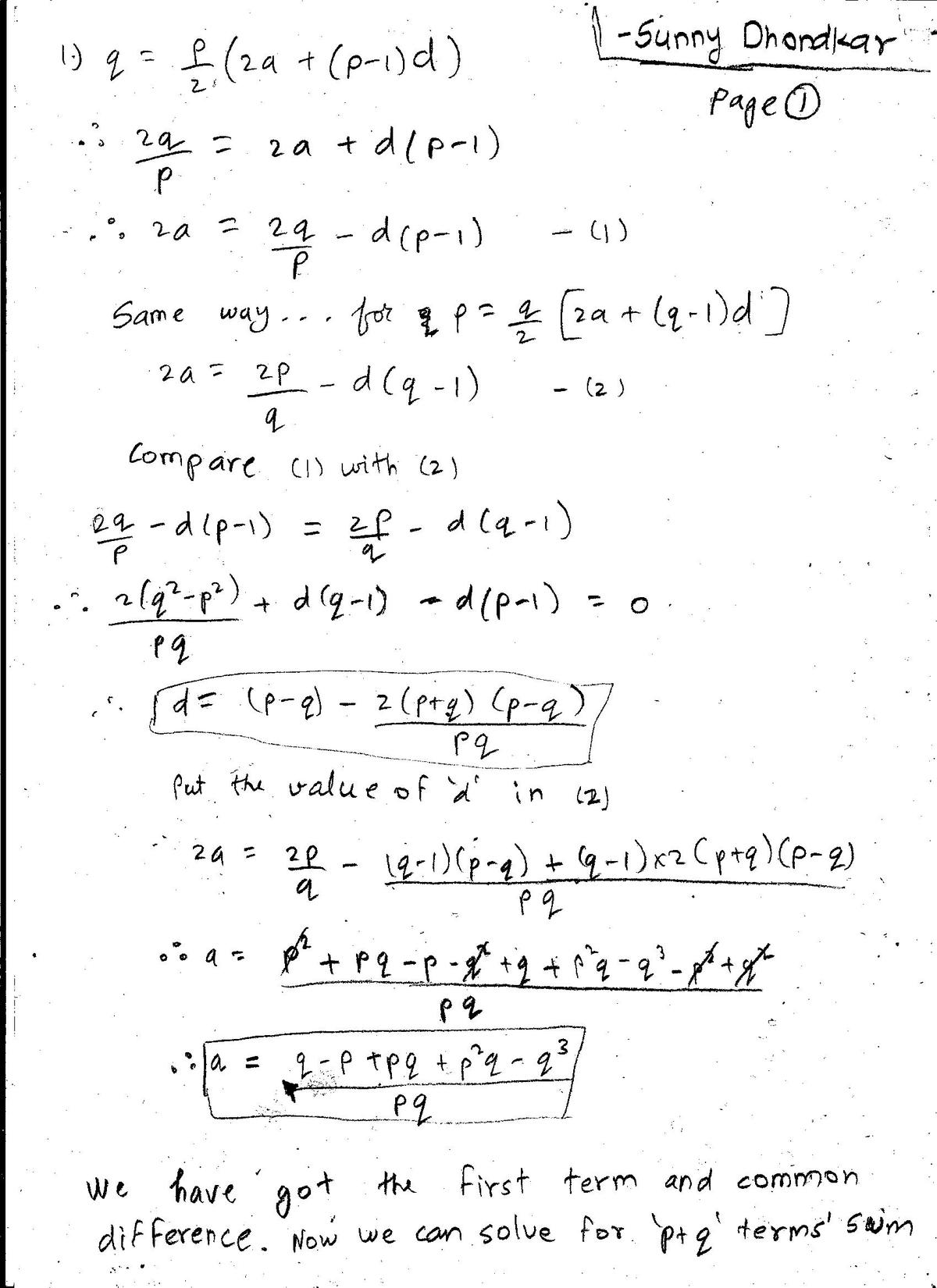
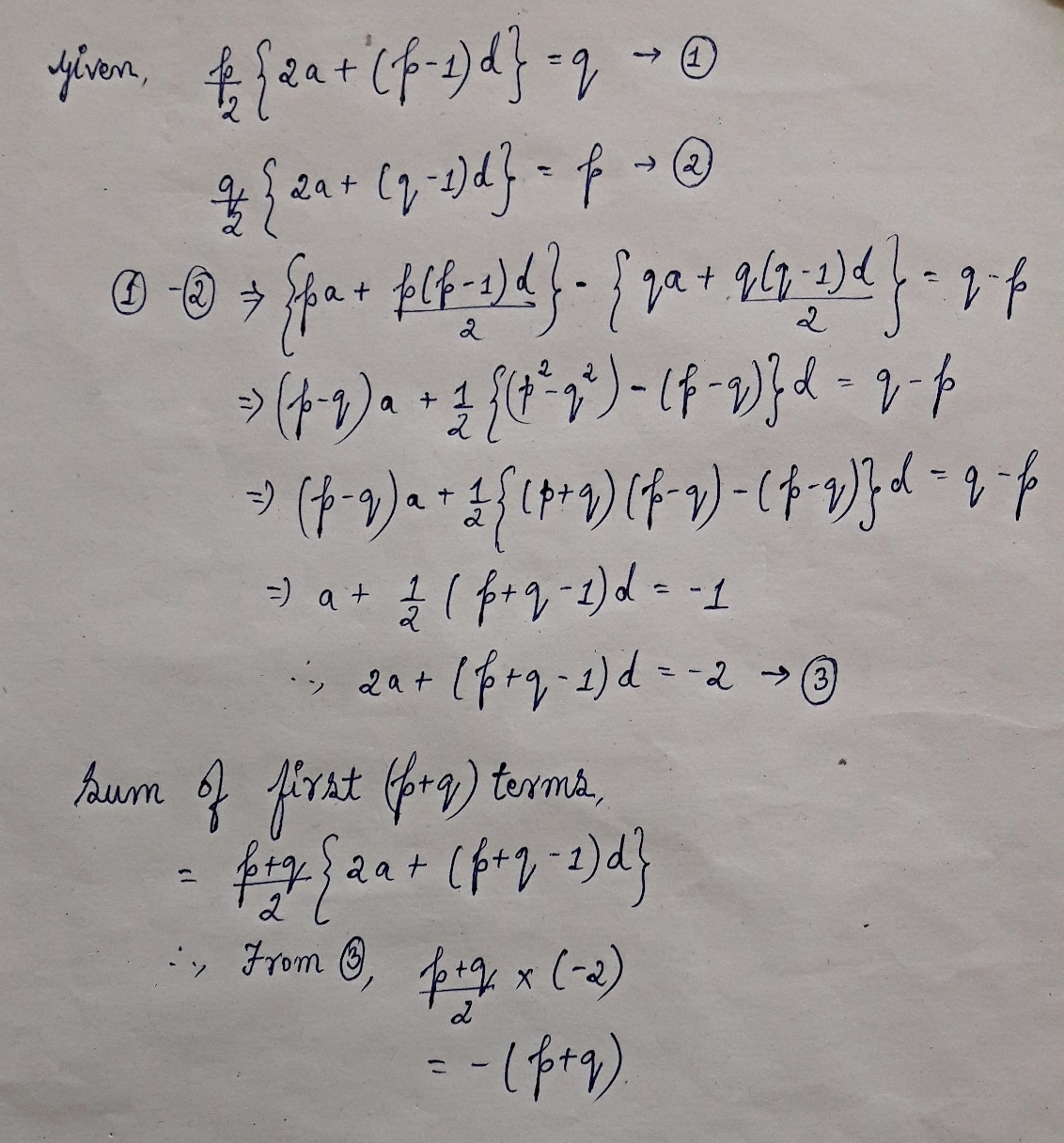
Relevant wiki: Arithmetic Progression Sum
Recall that the n th of an arithmetic progression is denoted by T n = a + ( n − 1 ) d , where a is the first term and d is the common difference. And the sum of the first n th terms of this progression is S n = 2 n [ 2 a + ( n − 1 ) d ] .
We have
S p = q 2 p ( 2 a + ( p − 1 ) d ) = q 2 a + ( p − 1 ) d = p 2 q S q = p 2 a + ( q − 1 ) d = q 2 p ( − ) 2 a + ( p − 1 ) d = p 2 q ⟹ ( q − 1 ) d − ( p − 1 ) d = q 2 p − p 2 q d ( q − p ) = p q 2 ( p 2 − q 2 ) − d ( p − q ) = 2 p q ( p + q ) ( p − q ) − d = p q 2 ( p + q ) d = p q − 2 ( p + q ) S p + q = 2 ( p + q ) ( 2 a + ( ( p − 1 ) + q ) d ) = 2 ( p + q ) ( 2 a + ( p − 1 ) d + q d ) = 2 ( p + q ) ( p 2 q + q p q − 2 ( p + q ) ) = 2 ( p + q ) ( p 2 q − p 2 p + 2 q ) = 2 p + q ( p − 2 p ) = − ( p + q )