An algebra problem by suresh jh
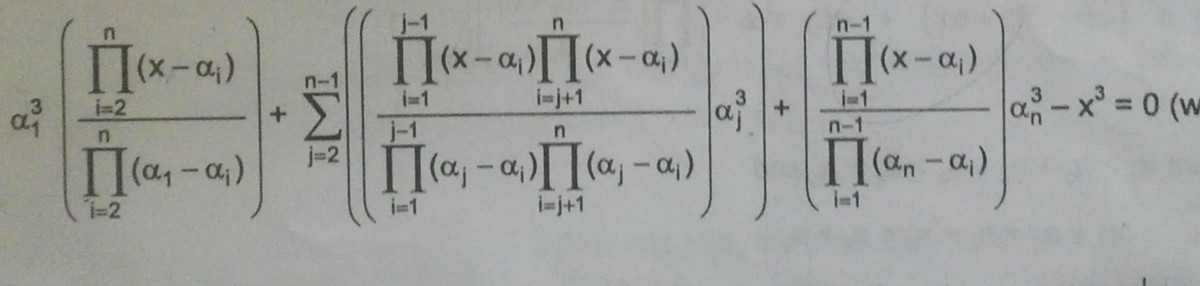 Find the number of solution of x?
Find the number of solution of x?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
All a i must be distinct or else there will be division by zero somewhere in the expression. Explanation: From the denominator of the leftmost additive term, ∏ i = 2 n ( α 1 − α i ) , we can immediately see that α 1 cannot be equal to any other α k (i.e., 2 ≤ k ≤ n ) because that would lead to division by zero. In particular, α 1 = α n . Now, we can direct our attention to the denominators produced by the summation, which are of the form: ∏ i = j ( α j − α i ) , where j ranges from 2 to n − 1 . From this, we can see that if α k = α i and k = i for any k , i such that 2 ≤ k ≤ n − 1 and 1 ≤ i ≤ n , then one of those denominators will be zero. Summing up these two conclusions, we deduce α i = α j for any pair i , j such that i = j .
If one substitutes a i for all 1 ≤ i ≤ n , then they are all zeros of the polynomial. Explanation: First, take x = α 1 . The entire expression reduces to α 1 3 + 0 + 0 − α 1 3 = 0 . Next take x = α k such that 2 ≤ k ≤ n − 1 . The entire expression reduces to 0 + α k 3 + 0 − α k 3 = 0 . Finally, taking x = α n , we get 0 + 0 + α n 3 − α n 3 = 0 . Therefore, α 1 , α 2 , . . . , α n are all roots of the equation.
Since a polynomial of degree n − 1 or less has n or more distinct zeros, then it must be the zero polynomial. Therefore, any x is a root of the equation.
Im not sure but , I have a idea about the solution and your solution doesn't match with it.
Log in to reply
Perhaps I should add some more details.
Log in to reply
I added some more details. Perhaps you'll be convinced now?
What you have on the LHS (other than the x 3 term is what's called a Lagrange Interpolation equation of y = x 3 given n points along the curve at x i = α i , y i = α i 3 .
Since the interpolation is of polynomial order n − 1 and it interpolates a cubic, which can be achieved with at most a cubic. The interpolation is over determined and as a result an infinite number of x 's will satisfy the equation.