An algebra problem by Vishnu Kadiri

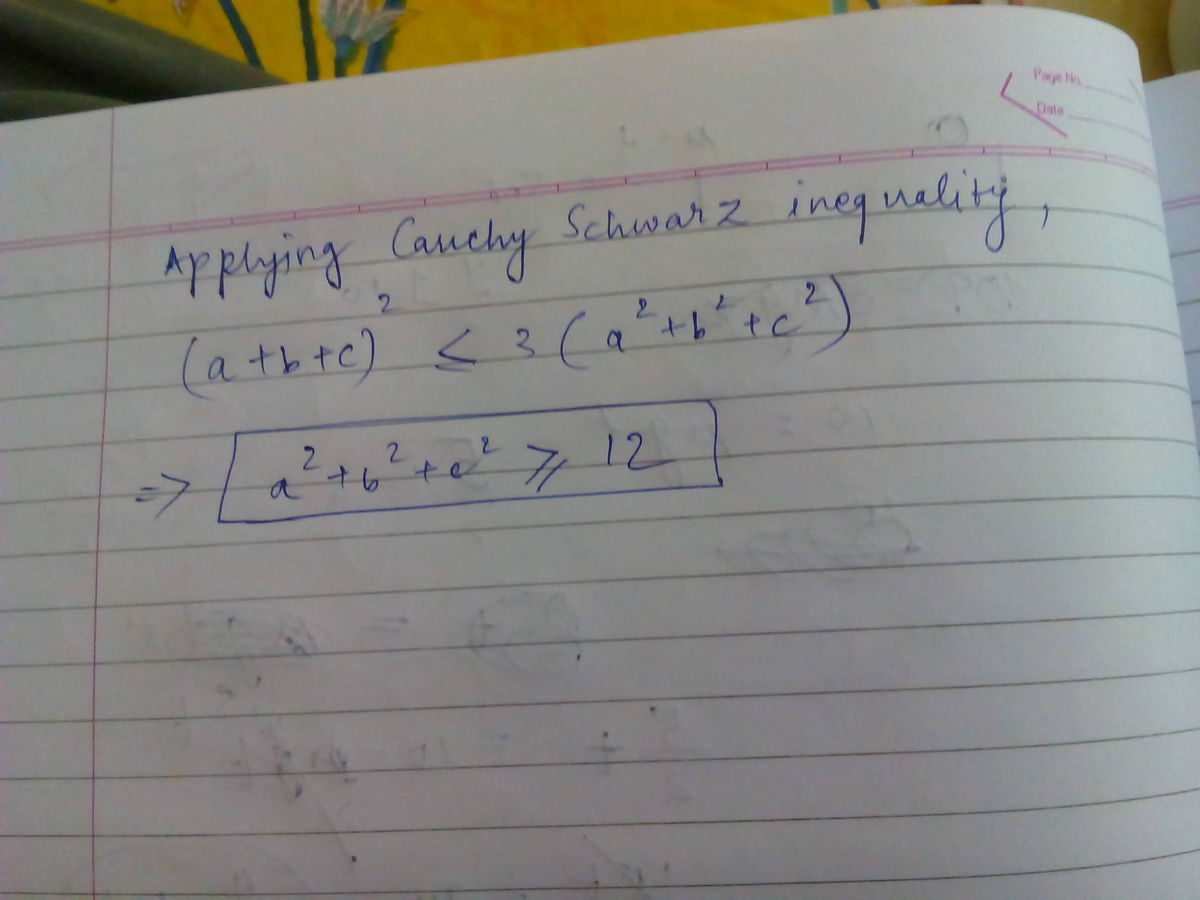
For $a, b, c > 0$ , we can use Cauchy-Schwarz inequality .

$\begin{aligned} (a+b+c)^2 & \le 3(a^2+b^2+c^2) \\ \implies a^2+b^2+c^2 & \ge \frac {6^2}3 = \boxed{12} \end{aligned}$

Note that if $a=0$ and $b, c >0$ the smallest $S = a^2+b^2+c^2 = 18 > 12$ , if $a < 0$ , then $S > 18$ . Similarly, if any two of $a$ , $b$ and $c$ are $\le 0$ , then $S \ge 36$ .