An Amphibious Car Would Be So Useful In This Problem.
 Benito the Bandit is hiding out in the center of a large circular lake of radius
3
0
miles. He has access to a speedboat, which can travel at a maximum speed of
3
0
miles per hour.
Benito the Bandit is hiding out in the center of a large circular lake of radius
3
0
miles. He has access to a speedboat, which can travel at a maximum speed of
3
0
miles per hour.
Police officer Parker arrived in his Chevrolet Impala police cruiser, with a court order to capture Benito the Bandit. He is a single officer, and is unable to drive (or swim, or fly) over the lake. He figures that the best way to capture Benito is to always drive towards the point on the shore which is closest to Benito.
What is the minimum integer speed at which Officer Parker would have to be able to drive, in order to be certain of catching Benito right when Benito reaches the shore?
The answer is 139.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
If you want to make that fraction look bigger, you can use \dfrac instead of \frac. For example, \frac{a}{b} produces b a while \dfrac{a}{b} produces b a . This proves much easier for fractions with more stuff going on, like this: 1 + r 2 − 2 r cos ( θ ) π + θ instead of 1 + r 2 − 2 r cos ( θ ) π + θ
In addition, you can use \ with the abbreviations for trigonometric functions to get them like the cos above. If trig represents a trigonometric or inverse trigonometric function, \trig will render.
Log in to reply
Thanks, Trevor, this is exactly what I'm looking for. Gotta get a hang of this Latex thing. I'll get around to expanding this solution. But, really, what's left is minimization of this fraction, which has to be done numerically anyway.
Log in to reply
Don't forget \cos in the denominator!
And if you want to center the fraction on the screen like this
1 + r 2 − 2 r cos ( θ ) π + θ
then you can replace \ ( and \ ) as delimiters with \ [ and \ ] but without the spaces of course. You don't have to use \dfrac or \displaystyle (which is used to make \int and \sum bigger) to make the fraction more visible. The above code was created with
\ [\frac{\pi+\theta}{\sqrt{1+r^2-2r\cos(\theta)}}\ ] again, without the spaces.
Daniel Liu created a handy LaTeX beginner's guide . You should check it out!
calvin is a genius!!!
Note: To display the diagram directly, just add "!" in front of the markdown link " title ". You can see the edit that I made to your solution.
Isn't markdown code wonderful :)
Log in to reply
Thanks Calvin, I think I'll be spending my time on Brilliant learning how to do this.
wow
really genius!!
This is a really fun problem. Just fleshing what is probably a slight variant of your solution out a bit, and noticing that the answer is independent of the radius R of the lake.
Parker may as well stay put at first, because at first Pete can travel fast enough to keep the center between him and Parker, and indeed move away from Parker. However, at a critical distance r from the center Pete will only just be able to keep pace angularly with Parker: 2 π r v = 2 π R V , and so r = V v R .
From this point, as Pete makes his way towards the perimeter, he will choose the angle θ from the original direction that maximizes the the advantage he has in time to the perimeter if he travels at that angle in a straight line. Using law of cosines to get Pete's distance,
Δ t = V π + θ − v R 1 + ( V v ) 2 − 2 V v cos ( θ )
Abbreviating the square root ⋯ ,
d t d Δ t = V R − V ⋯ R sin ( θ ) = V R ( 1 − ⋯ sin ( θ ) )
This is 0 when sin ( θ ) = ⋯ . Squaring that identity,
sin 2 ( θ ) = 1 + ( V v ) 2 − 2 V v cos ( θ ) ( V v ) 2 − 2 V v cos ( θ ) + cos 2 ( θ ) = 0 ( V v − cos ( θ ) ) 2 = 0 V v = cos ( θ )
Plugging this into the equation above for Δ t and setting that equal to 0, we quickly determine that t a n ( θ ) = π + θ , which makes θ = 1 . 3 5 2 and V = 1 3 8 . 1 1 , and so the answer is 1 3 9 .
This solution is under construction, while I learn how to do latex and stuff. First, the diagram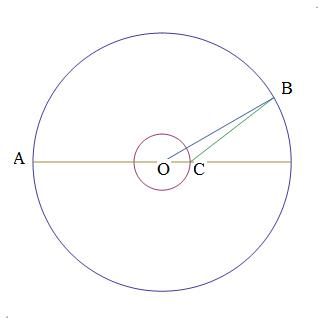 Lake, boat, car
Lake, boat, car
Okay, A and O are initial positions of car and boat. Let radius AO = 1, and OC = r, and let maximum speed of car = s. Benito tries to get as far away from the center O while keeping car, O, boat colinear. Eventually, Benito ends up going around circle of radius r = 30/s, after which he cannot get any closer to the shore without breaking colinearity of car, O, boat. Let's assume that at this point, Parker is back at A while Benito is at C, points A, O, C still being colinear. Then Benito must make a break for the shore at point B, just before Parker reaches that point. The ratio of distance CB must exceed or be equal to arclength AB times the ratio 30/s, which is r. Let ∠BOC = θ. Then we have this equation: (hold on---let me learn Latex now).
1 + r 2 − 2 r C o s ( θ ) π + θ
eh, let me work on this Latex thing a bit more. The point is, we wish to minimize this expression, which gives you the ratio r = 30/s that we seek. We end up with s = 30(4.60334...) = 138.1... approximately. I'll come back and improve on this solution, thank you for your patience.