An Angle Discovery!

Geometry Level 4

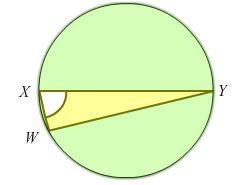Given that X Y XY is the diameter of the circle, where △ W X Y \triangle WXY is enclosed in the circle and that the ratio A r e a o f c i r c l e A r e a o f △ W X Y = 2 π \frac { Area\quad of\quad circle }{ Area\quad of\quad \triangle WXY } =2\pi .

Find the acute angle W X Y WXY . Giving your answer in degrees.


The answer is 75.

View wiki
Jonathan Xian Kuan Chee by Jonathan Xian Kuan Chee , 21, Singapore

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Let O O be the center of the circle, r r be the radius of the circle and ∠ W X Y = θ . \angle WXY = \theta. Then by the Central Angle Theorem we know that ∠ W O Y = 2 θ . \angle WOY = 2\theta.

The area of Δ W O Y \Delta WOY will then be r 2 sin ⁡ ( θ ) cos ⁡ ( θ ) . r^{2}\sin(\theta)\cos(\theta). But as Δ W O X \Delta WOX has the same base length, (namely r r ), and altitude as Δ W O Y \Delta WOY we see that the area of Δ W X Y \Delta WXY is exactly twice that of Δ W O Y \Delta WOY , i.e., 2 r 2 sin ⁡ ( θ ) cos ⁡ ( θ ) = r 2 sin ⁡ ( 2 θ ) . 2r^{2}\sin(\theta)\cos(\theta) = r^{2}\sin(2\theta).

From the given ratio we then have that

π ∗ r 2 r 2 sin ⁡ ( 2 θ ) = 2 π ⟹ sin ⁡ ( 2 θ ) = 1 2 , \dfrac{\pi*r^{2}}{r^{2}\sin(2\theta)} = 2\pi \Longrightarrow \sin(2\theta) = \dfrac{1}{2},

and so either 2 θ = 3 0 ∘ 2\theta = 30^{\circ} or 2 θ = 15 0 ∘ . 2\theta = 150^{\circ}. As ∠ X W Y = 9 0 ∘ \angle XWY = 90^{\circ} it is clear from the diagram that we are looking for θ > 4 5 ∘ , \theta \gt 45^{\circ}, so we chooses 2 θ = 15 0 ∘ ⟹ θ = 7 5 ∘ . 2\theta = 150^{\circ} \Longrightarrow \theta = \boxed{75^{\circ}}.

9 Helpful 0 Interesting 0 Brilliant 0 Confused

Ahh I didn't think about splitting the triangle into bits like that - good solution :) I took a slightly longer , more algebraic method

Curtis Clement - 6 years, 3 months ago

Log in to reply

Thanks. :) I like your approach too. There might be one or two other distinct ways of solving this problem; I'll give it some thought.

Brian Charlesworth - 6 years, 3 months ago

Here's another solution....(Sorry for not using Lattex)

Area of the circle = πr^2=(π x xy^2)/4 

(radius is xy/2)

Area of the triangle= 1/2 x base xheight=1/2 x WX x WY

Now it is given that

A r e a o f c i r c l e A r e a o f △ W X Y = 2 π \frac { Area\quad of\quad circle }{ Area\quad of\quad \triangle WXY } =2\pi

Use Pythagoras theorem.

XY^2 = WX^2 + WY^2

Then we get

X Y 2 XY^2 / WX x WY = 4.

Which is same as

(WX^2 + WY^2) / WX x WY = 4

This can be expresses as tanθ + 1/tanθ = 4 (where θ = angle WXY)

Now consider tanθ as x and solve. You will get a solution for x.

Take the inverse to get the angle.

Hari prasad Varadarajan - 6 years, 3 months ago

Log in to reply

Nice solution. Converting to tan ⁡ ( θ ) + 1 tan ⁡ ( θ ) = 4 \tan(\theta) + \dfrac{1}{\tan(\theta)} = 4 was a clever idea. :)

Brian Charlesworth - 6 years, 3 months ago

Great...I mess up the solution trying to solve in the bus commuting ride. However my approach is somewhat different. The triangle is always rectangle, being the hypotenuse the diameter so lenghts of sides are 2r \cos\theta and 2r \sin\theta. Then the area is half product of both. From that point is same as yours

Mariano PerezdelaCruz - 6 years, 3 months ago

One thing I am not clear is for the last step, how do you know that angle XWY is ninety degree. Can we solve if that angle is not specified assuming the picture is not accurate? As far as I think, both 15 snd 75 degrees are acute angle.

Shein Phyo - 6 years, 3 months ago

Log in to reply

Since X Y XY is a diameter, we know by Thales' theorem that ∠ X W Y = 9 0 ∘ . \angle XWY = 90^{\circ}.

Brian Charlesworth - 6 years, 3 months ago

Log in to reply

@Brian Charlesworth , thanks a ton for reminding me that theorem. I hadn't used that since middle school I didn't even think of it.

Shein Phyo - 6 years, 2 months ago
Pawan Kumar
Mar 12, 2015

Given: ∠ X W Y = 9 0 ∘ \angle XWY = 90^{\circ} (Thales' theorem) and Area of Δ W X Y = 1 2 r 2 \Delta WXY = \dfrac{1}{2}r^{2}

Let ∠ W X Y = θ \angle WXY = \theta and r = r = radius of the circle.

Since Δ W X Y \Delta WXY is right angled triangle:

Area of Δ W X Y = 1 2 × 2 r cos ⁡ ( θ ) × 2 r sin ⁡ ( θ ) \Delta WXY = \dfrac{1}{2}\times 2r\cos(\theta) \times 2r\sin(\theta) = 1 2 × 2 r 2 sin ⁡ ( 2 θ ) = \dfrac{1}{2} \times 2r^{2} \sin(2\theta)

= 1 2 r 2 = \dfrac{1}{2}r^{2} (Given).

⟹ sin ⁡ ( 2 θ ) = 1 2 \Longrightarrow \sin(2\theta) = \dfrac{1}{2}

⟹ 2 θ = 3 0 ∘ \Longrightarrow 2\theta = 30^{\circ} or 15 0 ∘ 150^{\circ}

⟹ θ = 1 5 ∘ \Longrightarrow \theta = 15^{\circ} or 7 5 ∘ 75^{\circ}

⟹ ∠ W X Y = 7 5 ∘ \Longrightarrow \angle WXY = 75^{\circ} (Judging from the diagram since ∠ W X Y > ∠ W Y X \angle WXY \gt \angle WYX )

1 Helpful 0 Interesting 0 Brilliant 0 Confused

I too did this way.

Niranjan Khanderia - 5 years, 11 months ago
Curtis Clement
Mar 9, 2015

Let WX = x {x} and let the radius of the circle be r {r} . By using A = 1 2 a b s i n ( θ ) \frac{1}{2}ab sin(\theta) and the fact that area of Δ \Delta WXY = r 2 2 \frac{r^2}{2} : A = 1 2 x . 2 r s i n ( θ ) = r 2 2 ⇒ r = 2 x s i n ( θ ) ( 1 ) A = \frac{1}{2}x.2r sin(\theta) = \frac{r^2}{2} \Rightarrow\ r = 2xsin(\theta) \ (1) Using Pythagoras Theorem; W Y = 4 r 2 − x 2 ⇒ 1 2 x 4 r 2 − x 2 = r 2 2 ⇒ 4 r 2 − x 2 = r 2 x WY = \sqrt{4r^2 - x^2} \Rightarrow\frac{1}{2}x\sqrt{4r^2 - x^2} = \frac{r^2}{2} \Rightarrow\sqrt{4r^2 - x^2} = \frac{r^2}{x} Squaring both sides and rearranging: r 4 − 4 x 2 r 2 + x 4 = 0 ⇒ ( r 2 − 2 x 2 ) 2 = 3 x 4 ⇒ r 2 = x 2 ( 3 + 2 ) r^4 -4x^2r^2 +x^4 = 0 \Rightarrow\ (r^2 -2x^2)^2 = 3x^4 \Rightarrow\ r^2 = x^2 (\sqrt{3} +2) Now substituting (1) into this equation: 4 x 2 S i n 2 ( θ ) = x 2 ( 3 + 2 ) ⇒ S i n 2 = 3 + 2 4 = 6 + 2 16 4x^2 Sin^2(\theta) = x^2(\sqrt{3} +2) \Rightarrow\ Sin^2 = \frac{\sqrt{3} +2}{4} = \frac{\sqrt{6} +\sqrt{2}}{16} ⇒ s i n ( θ ) = 6 + 2 4 \Rightarrow\ sin(\theta) = \frac{\sqrt{6} +\sqrt{2}}{4} ∴ θ = 75 \therefore\theta = 75

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...