An Ant's Journey

To find the shortest distance the ant must travel to reach the opposite bottom corner, we unfold the box. There are 3 ways to unfold the box: pulling out two $4 \times 6$ faces, pulling out a $4 \times 6$ face and a $4 \times 18$ face, or pulling out two $4 \times 18$ faces.

If we unfold the two $4 \times 6$ faces, the distance the ant travels is the length of the hypotenuse of a right triangle with side lengths $6$ and $26$ , which is $\sqrt{6^2 + 26^2}=\sqrt{712}$ .

If we unfold the $4 \times 6$ face and the $4 \times 18$ face, the distance the ant travels is the length of the hypotenuse of a right triangle with side lengths $10$ and $22$ , which is $\sqrt{10^2 + 22^2}=\sqrt{584}$ .

If we unfold the two $4 \times 18$ faces, the distance the ant travels is the length of the hypotenuse of a right triangle with side lengths $14$ and $18$ , which is $\sqrt{14^2 + 18^2}=\sqrt{520}$ .

Thus, the shortest path for the ant is by unfolding the two $4 \times 18$ faces, and $R^2$ is $520$ .

If the ant crawls only along the floor around the box, it will travel $6+18 = 24$ inches.

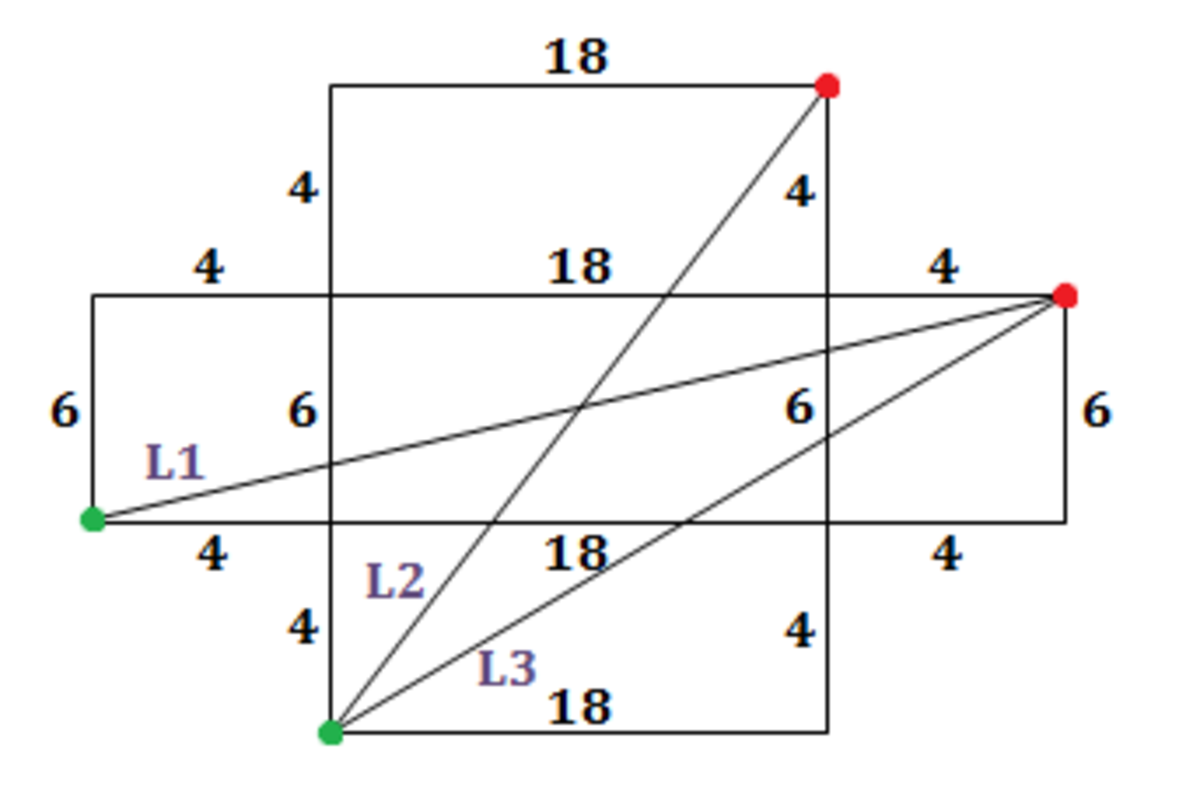
If the ant crawls on the box, consider the flattened version of the box (refer to the image above). The shortest distance would be a straight line across the rectangle. The ant can crawl along the diagonal of a $6 \times 26$ rectangle (L1), or a $14 \times 18$ rectangle (L2), or a $10 \times 22$ rectangle (L3). We use the Pythagorean theorem and find that the $14 \times 18$ rectangle has the shortest diagonal length, which is $\sqrt{520}$ . Since $520 < 576 = 24^2$ , this will be the shortest length. Thus, $R^2=520$ .

Let's open the box carton...Since the ant may not crawl under the box,neglect the undersurface..Note that straight line distance between any 2 points is the shortest possible.The ant's journey,as in the diagram, starts from A or B & ends in C or D. (In 3D box, A & B coincide at starting corner,and C & D coincide at opposite bottom corner.) So,however it crawls,it must follow paths AC,AD,BC or BD for shortest straightway paths.Applying Pythagoras' Theorem,observe that $AC^2=(18+4)^2 + (6+4)^2$ ; $AD^2=(18+ 4 \times 2)^2 + 6^2$ ; $BC^2=(6+ 4 \times 2)^2 + 18^2$ & finally $BD^2=(18+4)^2 + (6+4)^2$ . Thus, $BC^2=520$ is shortest..

$R=\sqrt{(4+6+4)^2+18^2}$

Two pairs of vertical faces are (6x4) and (18x4) - there are 3 cases a) open both 6x4 faces level with the top face 6x18, obtain a rectangle 6x30 b) open one 18x4 and one 6x4 face level with top face and consider hypotenuse of right angle triangle with perpendicular sides 10 and 22 c) open both 18x4 faces level with top face, obtain a rectangle 14x18 Case c) gives shortest path with R^2 = 14^2 + 18^2 = 520

We can fold the box out to make a "net" without the bottom face.

It is easy to see that the shortest path is either going over the 4 by 6, the top 6 by 18, and then on the second 4 by 6 face to the end point, or starting on the 4 by 18 face, going on the top of the 6 by 18, and then on the second 4 by 18 face.

These shortest paths are obviously lines, so we can use the pythagorean theorem to get that the two possible lengths are $\sqrt{520}$ or $\sqrt{712}$ .

Thus, $\sqrt{520}$ is the shorter value of R, so R^2 is equal to 520

(4+6+4)^2+18^2