A Geometric Application Of Differentiation
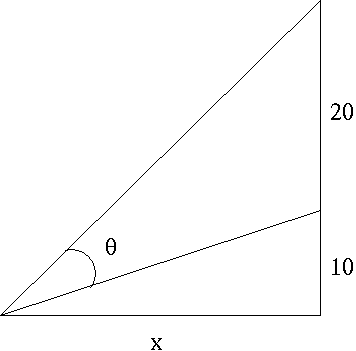
A movie screen on a wall is 20 feet high and 10 feet above the floor. At what distance x from the front of the room should you position yourself so that the viewing angle of the movie screen is as large as possible.
Also find the largest angle possible.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Short and standard approach...nice solution :)
Consider the circle passing through A and B and tangent to the line C E .
Then consider any other circle passing through A , B and cutting the line C E at two distinct points D and E .
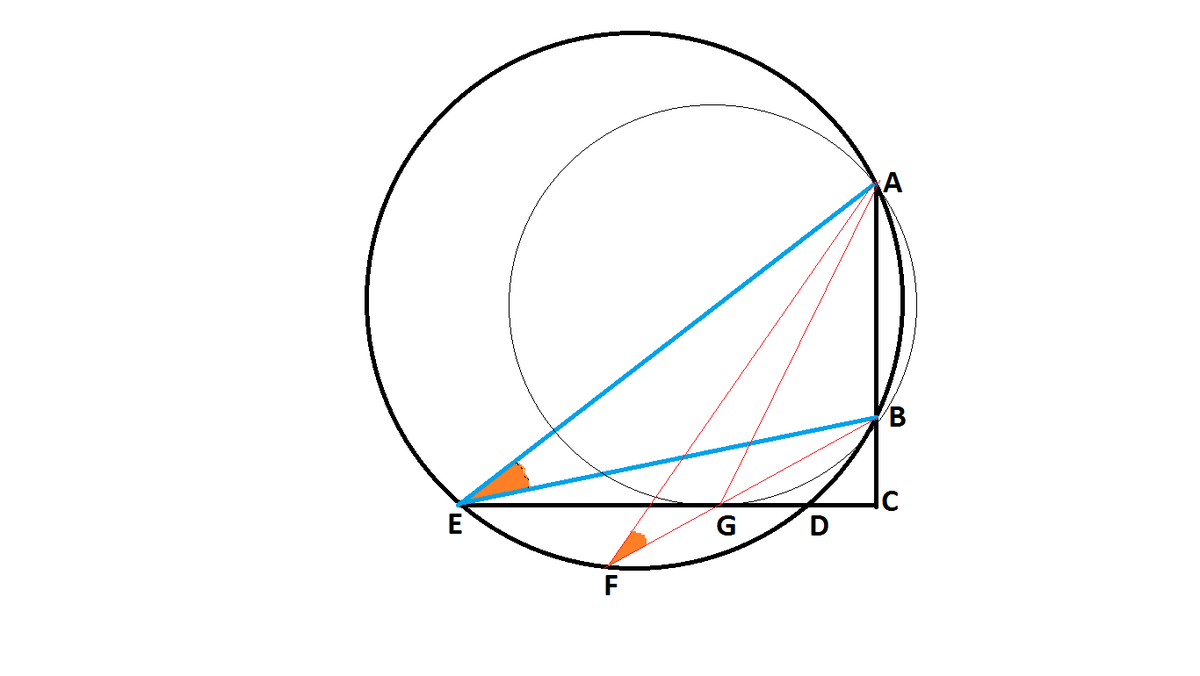
First we observe that any angle of viewing can be considered as the angle in the segment of the circumcircle of the triangle A B X where X is the point on C E where the observer is standing.
So all we have to do is optimize the angle in the segment subtended by all such circles.
Now we check that
m ( A E B ) = m ( A D B ) = m ( A F B ) ( as they are angles in the same segment of the bolder circle)
and m ( A F B ) = m ( A G B ) − m ( F A G ) < m ( A G B )
so that we have m ( A E B ) < m ( A G B )
(All the circles we consider should cut the circle at one point at least because the point(s) of intersection of the circle and the line C E denote the place where the person is standing)
So for all circles, the maximum angle is achieved when it is tangent to the line C E .
Now we use the power of point C with respect to the circle passing through A B G to get,
C A . C B = C G 2 , which yields x = 1 0 3 .
Now by alternate-segment theorem, we notice that m ( C G B ) = m ( B A G ) .
Also, in the right angled triangle G B C , we know the side lengths C B = 1 0 and C G = 1 0 3 so that we know the value of m ( C G B ) = 6 π and we have by Pythagoras' Theorem, G B = 2 0 = A B , so that B A G is an isosceles triangle with m ( A G B ) = m ( B A G ) = m ( B G C ) = 6 π .
Hence proved.
P.S. This problem is a beautiful example of how geometry can assist calculus.
That's why I loved this problem .... Nice solution ..
Solving θ in terms of x :
θ = arctan x 3 0 − arctan x 1 0
Differentiating with respect to x and setting equal to zero to find the maximum for θ :
0 = x 2 + 9 0 0 − 3 0 + x 2 + 1 0 0 1 0 , x = 3 0 0 = 1 0 3
Plugging this value of x into the function for θ to solve for the largest angle:
θ = arctan 3 − arctan 3 1 = 6 π = 3 0 ˚