An Area Problem: Find x
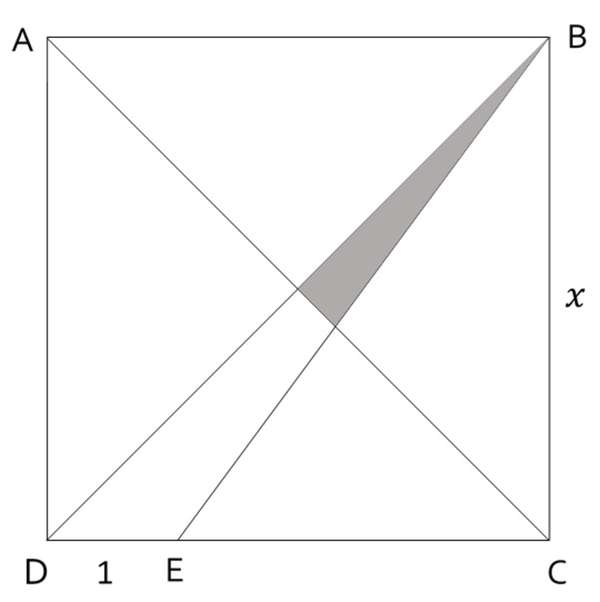
A B C D is a square with side length x and length D E is 1 . Find the value of x for which the area of the shaded region is 1 .
x can be written in the form a + b c where a , b , and c are positive integers with c being square free.
What is the value of a + b + c ?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Taking the point D as the origin, lines D C and D A along the x - and the y -axes respectively, we can write the vertices of the shaded triangle as ( 2 x , 2 x ) , ( 2 x − 1 x 2 , 2 x − 1 x 2 − x ) , ( x , x ) . So the area of this triangle is 4 ( 2 x − 1 ) x 2 . This is given to be 1 . So x = 4 + 2 3 (since x is greater than ∣ D E ∣ = 1 ), so that a = 4 , b = 2 , c = 3 and a + b + c = 9

Let A C intersects B D and B E at F and G respectively. Let G H = h be the altitude of △ B C G ; then H C = G H = h . We note that △ B G H is similar to △ B E C . Therefore we have:
E C G H x − 1 h ⟹ x 2 − ( 2 h + 1 ) x + h = B C B H = x x − h = 0 . . . ( 1 )
Given that area of the shaded region is 1 :
[ B F G ] [ B F C ] − [ B G C ] 4 x 2 − 2 h x ⟹ x 2 − 2 h x = 1 = 1 = 1 = 4 . . . ( 2 )
Then we have ( 2 ) − ( 1 ) : x − h = 4 ⟹ h = x − 4 and:
( 2 ) : x 2 − 2 ( x − 4 ) x − 4 − x 2 + 8 x − 4 x 2 − 8 x + 4 = 0 = 0 = 0
⟹ x = 2 8 + 6 4 − 1 6 = 4 + 2 3
Therefore a + b + c = 4 + 2 + 3 = 9 .