An Arrowhead
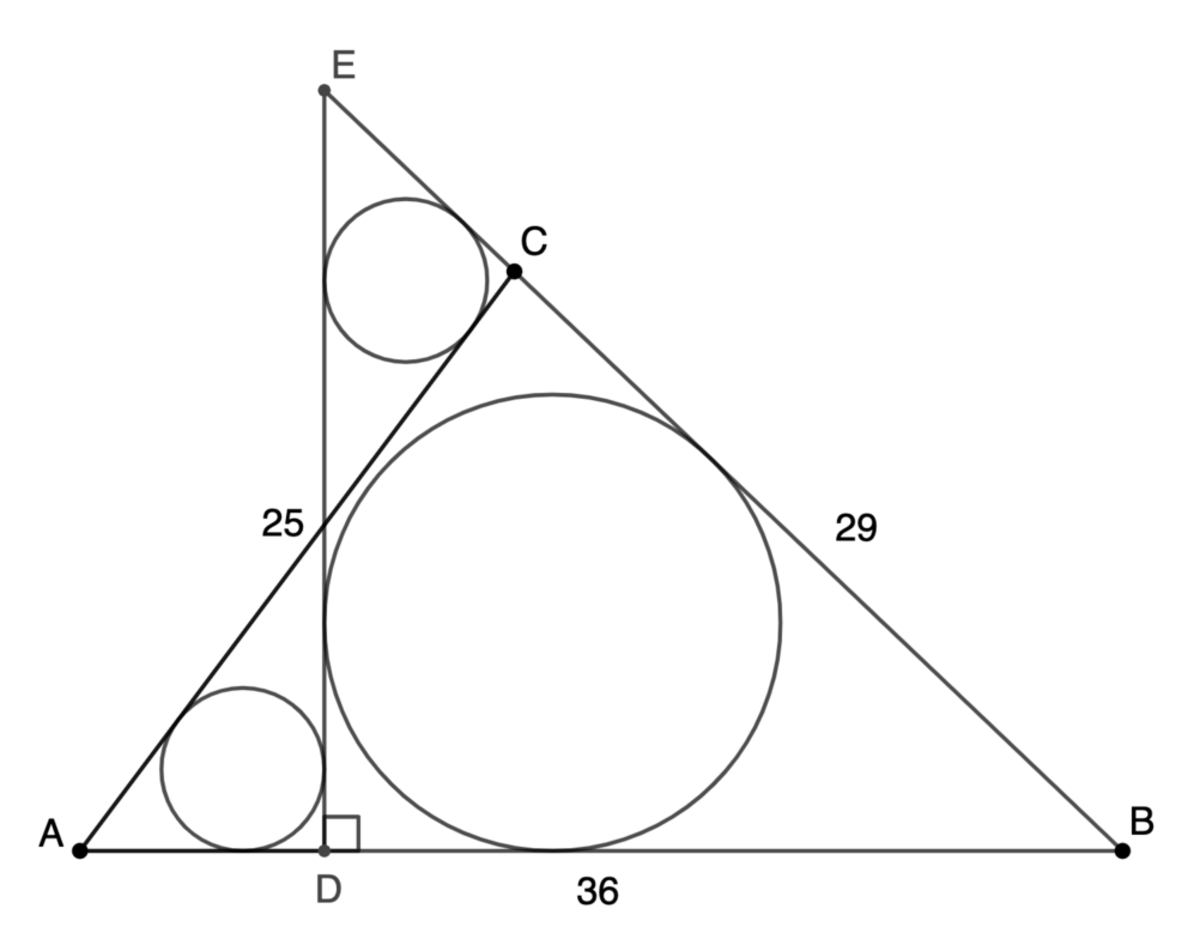
A C = 2 5 , A B = 3 6 , C B = 2 9 , E D ⊥ A B . The two small circles are congruent. If the radius of the large circle, R = q p , where p and q are coprime positive integers, submit p + q .
The answer is 71.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
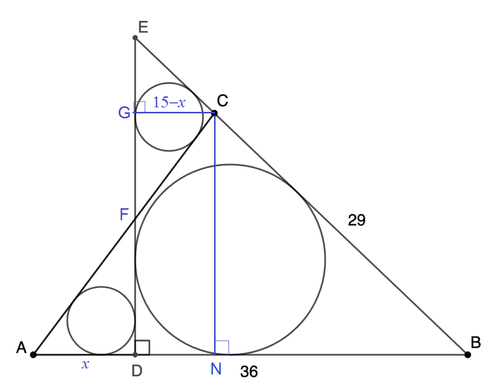
First we find that altitude C N = 2 0 , A N = 1 5 , and N B = 2 1 . Then △ A C N is a 3 - 4 - 5 right triangle and △ B C N , a 2 0 - 2 1 - 2 9 right triangle.
Let A D = x . Then D F = 3 4 x , where F is the intersection point of A C and D E , and A F = 3 5 x . Since inradius of a triangle, r = s A , where A and s are the area and semi-perimeter of the triangle, then the radius of the two congruent circles
r = A D + D F + F A A D ⋅ D F = x ( 1 + 3 4 + 3 5 ) 3 4 x 2 = 3 x
Let C G be perpendicular to D E . Then C G = A N − A D = 1 5 − x . Then C E = 2 1 2 9 ( 1 5 − x ) , E G = 2 1 2 0 ( 1 5 − x ) , G F = 3 4 ( 1 5 − x ) , and F C = 3 5 ( 1 5 − x ) . Then
r = C E + E F + F C C G ⋅ E F = 2 1 2 9 + 2 1 2 0 + 3 4 + 3 5 ( 1 5 − x ) ( 2 1 2 0 + 3 4 ) = 7 3 ( 1 5 − x ) 3 x 7 x ⟹ x = 7 3 ( 1 5 − x ) = 1 3 5 − 9 x = 1 6 1 3 5
Then the radius of the large circle,
R = B D + D E + E B D E ⋅ B D = 1 + 2 1 2 0 + 2 1 2 9 ( 3 6 − x ) ⋅ 2 1 2 0 = 8 6 3
Therefore p + q = 6 3 + 8 = 7 1 .
Draw in the following segments:
△ A B C is a 1 5 - 2 0 - 2 5 right triangle combined with a 2 0 - 2 1 - 2 9 right triangle, so that A H = 1 5 , C H = 2 0 , A C = 2 5 , B H = 2 1 , and B C = 2 9 .
Let G C = x , so that A G = A C − G C = 2 5 − x . Since △ A D G ∼ △ C F G ∼ △ A H C by AA similarity, F G = A C C H ⋅ G C = 5 4 x , F C = A C A H ⋅ G C = 5 3 x , G D = A C C H ⋅ A G = 5 4 ( 2 5 − x ) , and A D = A C A H ⋅ A G = 5 3 ( 2 5 − x ) .
Since △ E F C ∼ △ C H B by AA similarity, E F = H B C H ⋅ F C = 7 4 x and E C = H B C B ⋅ F C = 3 5 2 9 x , which means E G = E F + F G = 7 4 x + 5 4 x = 3 5 4 8 x .
The inradius of right △ A D G is r 1 = 2 1 ( A D + G D − A G ) = 2 1 ( 5 3 ( 2 5 − x ) + 5 4 ( 2 5 − x ) − ( 2 5 − x ) ) = 5 1 ( 2 5 − x ) .
And the inradius of △ E G C is r 2 = E G + E C + G C 2 ⋅ 2 1 ⋅ E G ⋅ F C = 3 5 4 8 x + 3 5 2 9 x + x 2 ⋅ 2 1 ⋅ 3 5 4 8 x ⋅ 5 3 x = 3 5 9 x .
Since the two small circles are congruent, r 1 = r 2 , so 5 1 ( 2 5 − x ) = 3 5 9 x , which solves to x = 1 6 1 7 5 .
Then:
D B = A B − A D = 3 6 − 5 3 ( 2 5 − x ) = 3 6 − 5 3 ( 2 5 − 1 6 1 7 5 ) = 1 6 4 4 1
E D = E G + G D = 3 5 4 8 x + 5 4 ( 2 5 − x ) = 3 5 4 8 ⋅ 1 6 1 7 5 + 5 4 ( 2 5 − 1 6 1 7 5 ) = 4 1 0 5
E B = E C + C B = 3 5 2 9 x + 2 9 = 3 5 2 9 ⋅ 1 6 1 7 5 + 2 9 = 1 6 6 0 9
That means the inradius of △ E D B is R = 2 1 ( D B + E D − E B ) = 2 1 ( 1 6 4 4 1 + 4 1 0 5 − 1 6 6 0 9 ) = 8 6 3 .
Therefore, p = 6 3 , q = 8 , and p + q = 7 1 .