A Kirchhoff Voltage and Current Law problem.
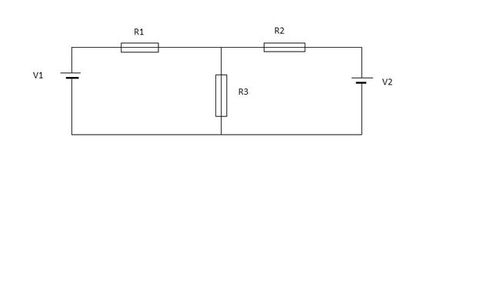 Find the voltage across the 40 ohm resistor.
Find the voltage across the 40 ohm resistor.
Following values are to be used: R 1 = 1 0 Ω , R 2 = 2 0 Ω , R 3 = 4 0 Ω , V 1 = 1 0 V , V 2 = 2 0 V .
Answer is to be given in volts.
The answer is 11.44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Using Mesh Analysis, let V be the voltage across the 40 ohm resistor.
1 0 1 0 − V = I 1
2 0 2 0 − V = I 2
Adding the two equations,
I 1 + I 2 = 2 0 1 ( 4 0 − 3 V )
Since,
V = 4 0 ( I 1 + I 2 )
Thus,
V = 8 0 − 6 V
V = 7 8 0 ≈ 1 1 . 4 4
(10 - v)/ 10 + (20 - v)/ 20 = v/ 40
(40 - 4 v)/ 40 + (40 - 2 v)/ 40 = v/ 40
80 - 6 v = v
7 v = 80
v = 80/ 7 = 11.428571428571428571428571428571+
Checked that 0.428571 = 0.142857 + 0.285714 that the direction of current becomes opposite for R1.
The whole circuit presents an only set of voltages and currents.
Answer: 11.428571428571428571428571428571+
using kirchoff's law in the first loop containing v1 equation is 5i1+4i2=1 applying kirchoff's law in the second loop containing v2 equation is 2i1+3i2=1 solving both equation we have i1=(-1/7) i2=(3/7) current passing through 40 ohm resistor is 2/7 using ohm's law v=ir v=2/7x40=80/7
We can use voltage superimposition to solve this problem.
Therefore, the voltage across R 3 , V 3 = V 3 1 + V 3 2 = 7 8 0 = 1 1 . 4 4 V.