Wayward times
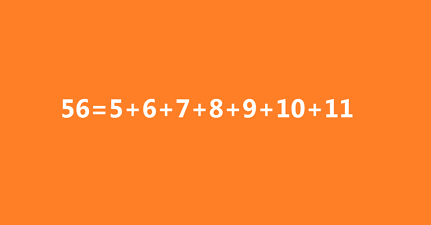 Let
S
be the set of positive integers, that cannot be written as a sum of at least 2 consecutive positive integers.
Let
S
be the set of positive integers, that cannot be written as a sum of at least 2 consecutive positive integers.
For example 10 can be written as: 1 0 = 1 + 2 + 3 + 4 .
1 cannot be expressed in such a way and thus is in the S .
Now build the multiplicative inverse of all the members of S , add them all up and then type the result in your answer field.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Note that i = 1 ∑ n i = 2 n ( n + 1 ) , which means that 1 + 2 + ⋯ + n = 2 n ( n + 1 ) .
Also note that:
- ( m + 1 ) + ( m + 2 ) + ⋯ + n
- = [ 1 + 2 + ⋯ + n ] − [ 1 + 2 + ⋯ + m ]
- = i = 1 ∑ n i − i = 1 ∑ m i
- = 2 n ( n + 1 ) − 2 m ( m + 1 )
- = 2 1 [ n ( n + 1 ) − m ( m + 1 ) ]
- = 2 1 [ n 2 + n − m 2 − m ]
- = 2 1 [ n 2 − m 2 + n − m ]
- = 2 1 [ ( n − m ) ( n + m ) + ( n − m ) ]
- = 2 1 [ ( n − m ) ( n + m + 1 ) ]
Note that exactly one of ( n − m ) and ( n + m + 1 ) is odd.
Also note that N must be written as a sum of at least 2 consecutive positive integer, so n − m ≥ 2
Let N = 2 r x where x is odd and r is a non-negative integer.
We try to write N in the form of 2 1 [ ( n − m ) ( n + m + 1 ) ] : N = 2 r x = 2 1 ( 2 r + 1 x )
Note that the second term, ( n + m + 1 ) , must be bigger than the first term, ( n − m ) .
CASE ONE:
If 2 r + 1 > x , then: { n − m = x n + m + 1 = 2 r + 1 ⟹ { n = 2 2 r + 1 + x − 1 = 2 r + 2 x − 1 m = 2 2 r + 1 − x − 1 = 2 r − 2 x + 1
Also, n − m ≥ 2 :
- ( 2 r + 2 x − 1 ) − ( 2 r − 2 x + 1 ) ≥ 2
- 2 x − 1 + 2 x + 1 ≥ 2
- x ≥ 2
- which means that x cannot be 1 , which means that N cannot be 2 a .
CASE TWO:
If 2 r + 1 < x , then: { n − m = 2 r + 1 n + m + 1 = x ⟹ { n = 2 2 r + 1 + x − 1 = 2 r + 2 x − 1 m = 2 − 2 r + 1 + x − 1 = − 2 r + 2 x − 1
Also, n − m ≥ 2 :
- ( 2 r + 2 x − 1 ) − ( − 2 r + 2 x − 1 ) ≥ 2
- 2 r + 1 ≥ 2
- r ≥ 0
- which does not generate any further limitation.
THEREFORE:
The only requirement for N is that it is not an integral power of 2 , or N = 2 a .
Therefore, S contains only 2 a .
Therefore, the required sum:
- = 2 0 1 + 2 1 1 + 2 2 1 ⋯
- = 1 1 + 2 1 + 4 1 + 8 1 + ⋯
- = I
- ⟹ 2 I = 1 2 + 2 2 + 4 2 + 8 2 + ⋯
- ⟹ 2 I = 2 + 1 1 + 2 1 + 4 1 + ⋯
- ⟹ 2 I = 2 + I
- ⟹ I = 2
Appendix:
Its convergence can be demonstrated by the fact that the ratio between the next term to the current term is always 2 1 , which is between − 1 and 1 .
Suppose that positive integer N can be written as a sum of n consecutive positive integers starting with m + 1 , where n ≥ 2 and m ≥ 0 : N = m + 1 + m + 2 + . . . + m + n = m n + 2 n ( n + 1 ) Which gives 2 N = n ( n + 2 m + 1 ) ⋆ . RHS of ⋆ is two factors greater than 1 with different parity, so N cannot be a power of 2 .
For N = a b with a > 1 odd and b even, set n = a and m = 2 2 b − a − 1 . For odd numbers greater than 1 , N = 2 k + 1 with k ≥ 1 , one can see easily that N = k + k + 1 . Therefore S = { 1 , 2 , 2 2 , 2 3 , . . . } and 1 + 2 1 + 2 2 1 + . . . = 2 .