An Electric Pendulum and a Uniform Magnetic Field *NO CORRECT ANSWER*
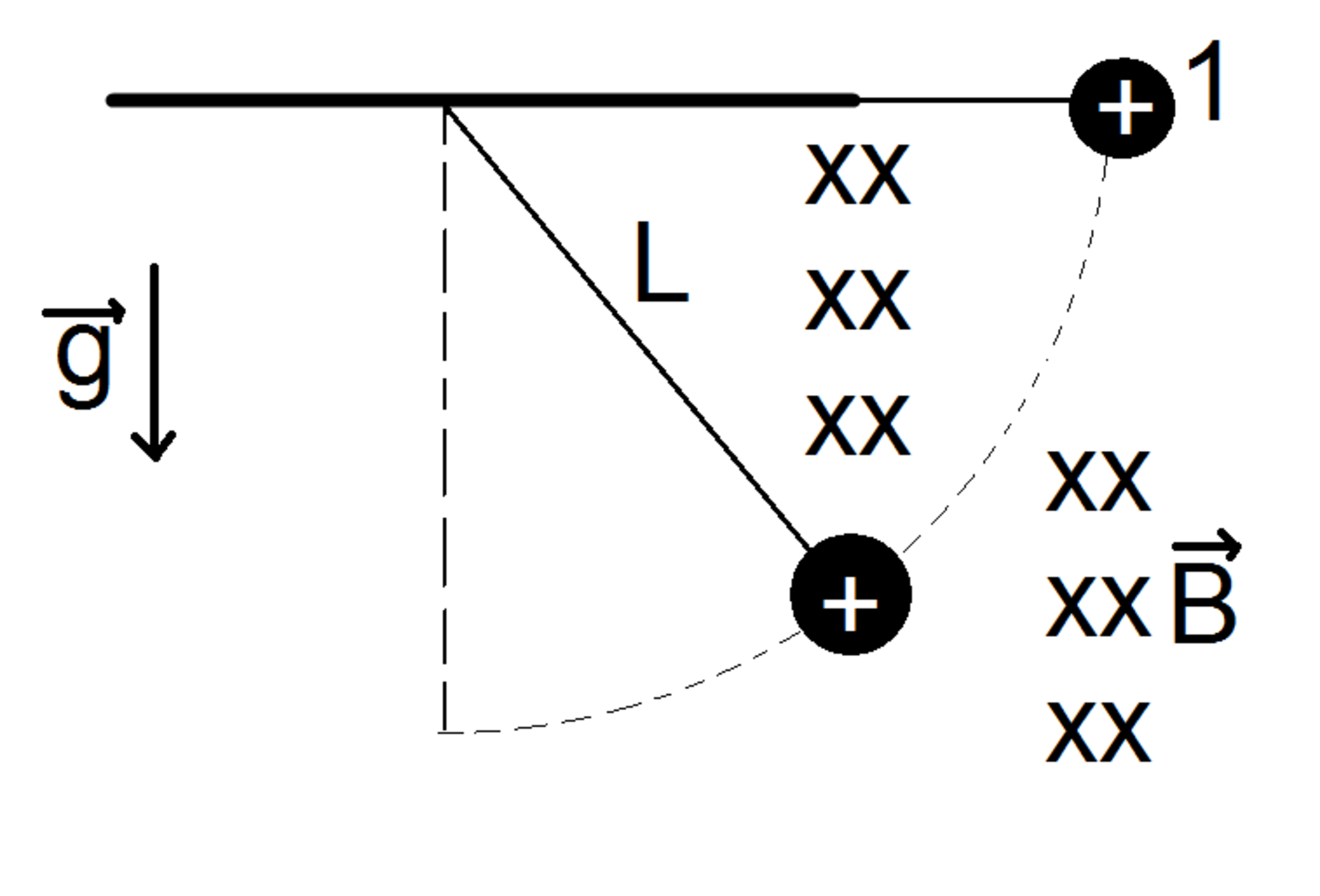
The figure shows an electric pendulum consisting of a wire of length L = 1m connected to a sphere of mass m = 5kg and positive charge q = 2C in a region containing a uniform gravitational field g = 10m/s² and a uniform magnetic field B = 15T perpendicular to the plane of the paper. The maximum traction supported by the wire is T = 240N. The ball is abandoned from rest from position 1. Find the maximum
HEIGHT
h traveled by the sphere until the wire breaks.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let θ be the angle that the wire forms with the vertical, after the sphere has dropped a height h relative to position 1. At that time, the sphere has already reached a speed v = √2gh.
From Newton's second law, in the radial direction, we have:
T - mgcosθ - qvB = mv² / L
T - mgcosθ - qB√2gh = 2mgh / L
cosθ = h / L
T = 3mgh / L + qB√2gh
240 = 150h + 30√20h
8 = 5h + √20h
25h² - 100h + 64
h < L
h = 0.4m
(NO ANSWERS) SORRY!!!