A powerful circuit
Electricity and Magnetism
Level
2
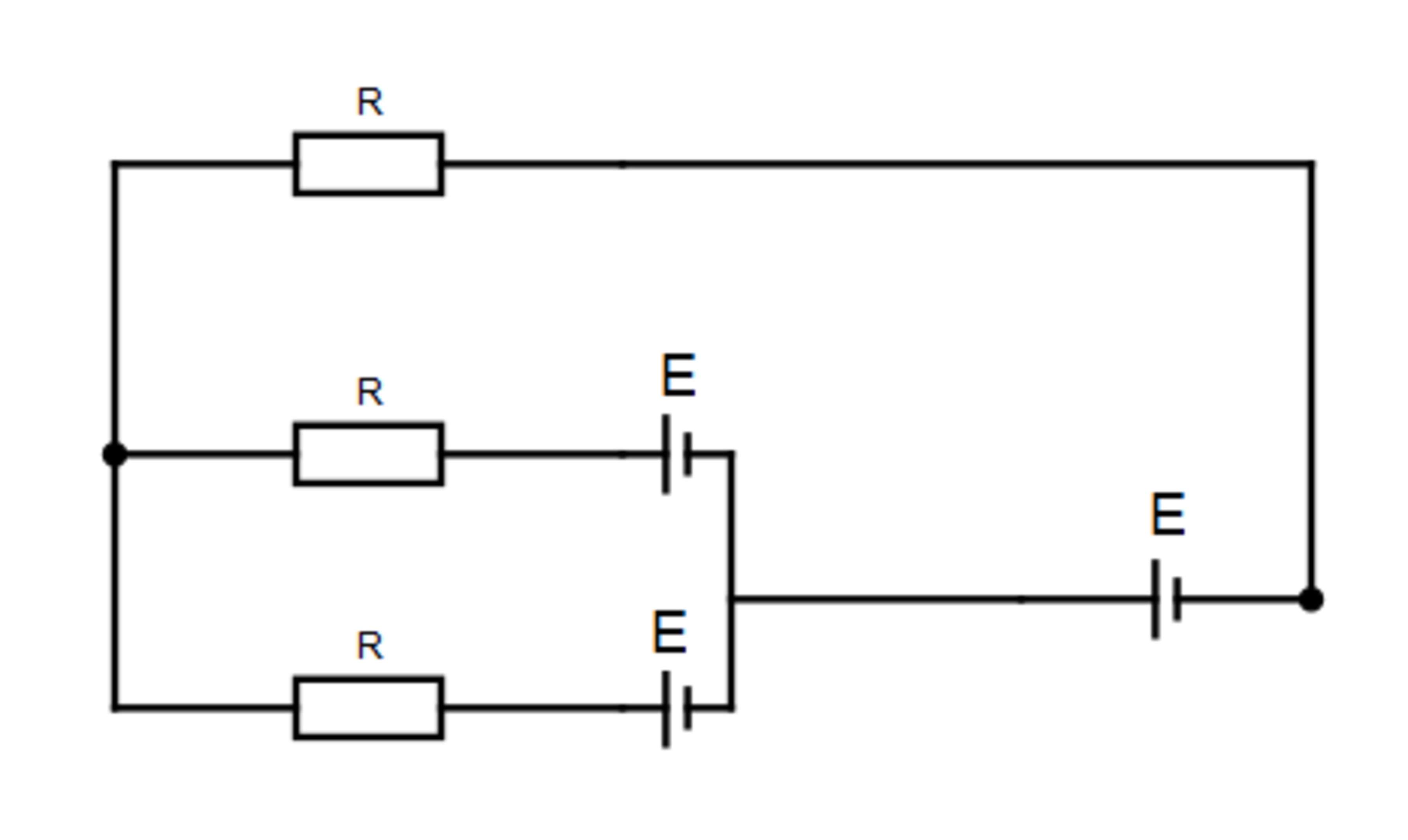
What is the total power of all of the resistors on the picture?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
On the picture above, I have assumed the directions of the currents I 1 , I 2 , and I . Using Kirchoff's First Law, we can see that I = I 1 + I 2 . I have also marked points A and B. We can see that they have the same potentials, meaning that U a b = 0 . U a b can also be expressed as E − E − R ∗ I 2 − R ∗ I 1 , meaning that I_1 = I_2 = \(\frac{I}{2} ). U a b can also be expressed as E − R ∗ I − R ∗ I 1 + E . Switching I with \(\frac{I_1}{2} ) gives us an equation from which we can express I 1 as \(\frac{2E}{3R} ), and that is also equal to I 2 . The total power is equal to the sum of all of the powers on the resistors, and is equal to 2*R*I_1^2 + R*I^2 = \(\frac{8E^2}{3R} ).