An electricity and magnetism problem by Miraj Shah

Electricity and Magnetism Level 3

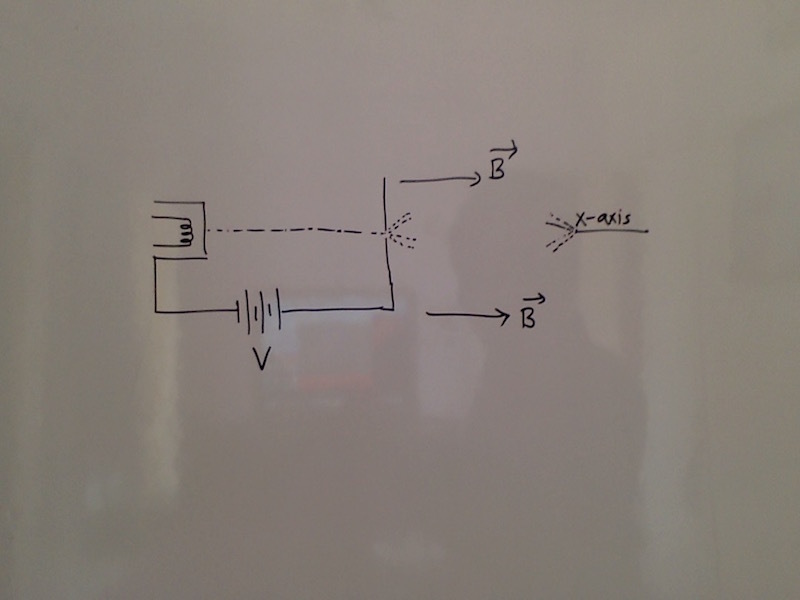
Electrons are ejected from the electron gun with negligible velocity. These emitted electrons are then accelerated across a potential difference $V$ along the $x$ -axis. These electrons emerge from a narrow hole into a region of uniform magnetic field $B$ . However, some of the electrons emerging from the hole make slightly divergent angles as shown in the figure above. If the paraxial electrons are refocused on the $x$ -axis. at a distance $\sqrt{\dfrac{A \pi^2 mV}{eB^2}}$ from the hole, then find the value of $A$ .

Notations :

$m$ deontes the mass of electron.
$e$ denotes the magnitude of charge on an electron.

The answer is 8.

1 solution

Erasmo Hinojosa
Apr 30, 2016

Since the electrons emerge in some direction that it is not necesarly parallel to the x-axis, their velocities would have (as understood from the image) two components (it doen't have a velocity component in or out of the page). Now, the magnetic field is parallel to the x-axis son the electron would follow helicoidal paths with the velocity perpendicular to the x-axis changing direction but maintaing the same maginitud (circle in the y-z plane). Considering that the electron, while emerging, forms an angle $\theta$ with the x-axis and using $sin \theta=\theta$ and $cos \theta=1$ (paraxial aproximation) and considering the forces and energy:

$D=v_x T=vcos \theta T=v T$ (distance)

$R=\frac{mv \theta} {eB}$ (radius of circunference in the y-z plane)

$T=\frac {2 \pi R} {v \theta}=\frac {2 \pi m} {eB}$ (period)

$v=\sqrt{\frac{2eV} {m}}$

$D=\sqrt{\frac {8 \pi^2 m V} {e B^2}}$

Comparing to the expression of the questio yields:

$A=8$

Please make it easy to understand How do u take time to be time period

Pratham Dhiman - 10 months ago

An electricity and magnetism problem by Miraj Shah

The answer is 8.

1 solution

0 pending reports