How many will succeed?

Electricity and Magnetism Level 3

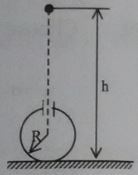Electrically charged drops of mercury fall from an altitude h h into a spherical metal vessel of radius R R in the upper part of which there is a small opening. The mass of each drop is m m and the charge of the drop is q q . The number n n of the last drop that can still enter the sphere is n ∗ 2 π ϵ 0 m g ( h − R ) R q 2 \large n*2\pi \epsilon_0 \frac{mg(h-R)R}{q^2} . Then what is the value of n n ?


The answer is 2.

Nishant Rai by Nishant Rai , 25, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Pulkit Gupta
Sep 12, 2015

With each charge that enters the metallic sphere, a radially outward electric field starts building up. ( since charge is positive)

When the force due to the electric field at the opening of the sphere balances the gravitational force on the charged particle, charges would remain suspended and no new charge shall enter.

Let n be the number of the last charge that enters the sphere. Then net charge of sphere at that time is nq. Therefore, electric field at that time at the opening of the sphere is (1 / 4 pi epsilon) nq/ R^2

Since, F = qE ; force on a charged particle near spherical opening is q * (1/4 pi epsilon) nq / R^2. This force should be equal to mg. Also R= h-R , R^2 = R ( h - R ). Compute the value of n from the above equations.

6 Helpful 1 Interesting 0 Brilliant 5 Confused

How is R = h − R R = h-R ?

Ankit Kumar Jain - 3 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...