An electricity and magnetism problem by Soumava Pal
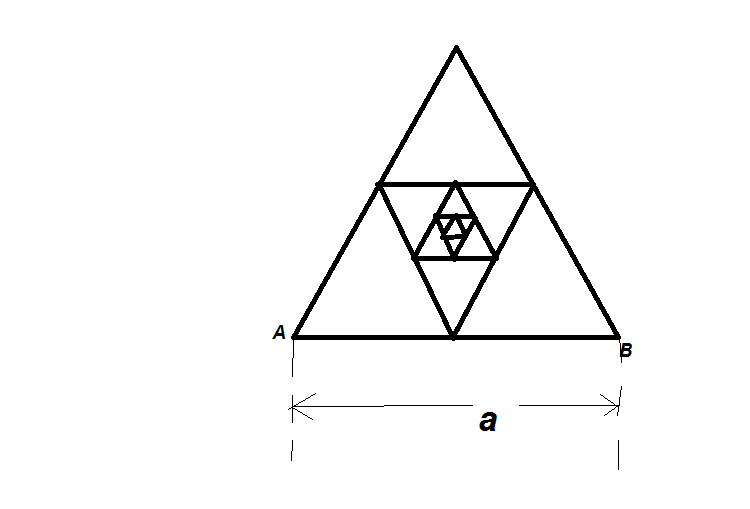
Determine the resistance R A B between points A and B of the frame made of thin homogeneous wire assuming that the number of triangles (with sides decreasing by half) tends to infinity. (All the triangles are equilateral.) Side A B = a = 1 unit , and the resistance of unit length of the wire is 1 unit.
The answer is 0.54858.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
:p Yeah right.
Since the circuit is symmetrical, we can just do it by setting up a relation with the resistance between the second inner triangle and the outermost triangle. So we replace the second inner triangle that is the medial triangle of the medial triangle of the outermost triangle by a resistance R A B / 2 . Now let R A B =r, then if the resistance of AB is R, we have,
r = R ( R + R + 2 r R r / 2 ) ( R + R + R + 2 r R r / 2 ) − 1
Solving this equation yields,
r = R 3 7 − 1
Here R=1. So answer is simply, 3 7 − 1
U missed to mention that as the distribution of current is symmetric you can plug up the node and then proceed