An electricity and magnetism problem by Sudeep Salgia
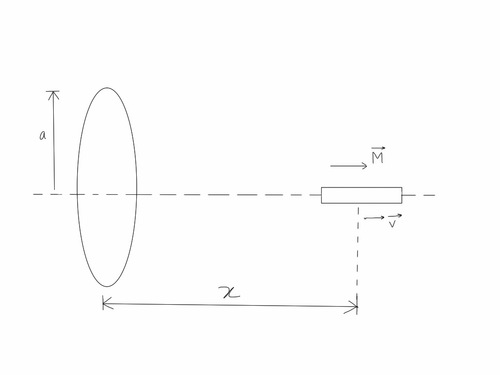 Along the axis of a fixed small loop of resistance
, a short bar magnet with dipole moment
is moved away from it with a velocity
. The
is oriented such that it points away from the ring as shown in the figure. Given that the radius of the loop is
and distance of the magnet from the center of the loop is
, then the magnitude of the force of interaction between the loop and the bar magnet can be writen as
where
are natural numbers with
and
coprime.
Along the axis of a fixed small loop of resistance
, a short bar magnet with dipole moment
is moved away from it with a velocity
. The
is oriented such that it points away from the ring as shown in the figure. Given that the radius of the loop is
and distance of the magnet from the center of the loop is
, then the magnitude of the force of interaction between the loop and the bar magnet can be writen as
where
are natural numbers with
and
coprime.
Find the value of
.
Details and Assumptions:
-
The bar magnet is short and .
-
is the permeability of vacuum.
-
The magnetic field due to the magnet can be considered almost parallel to the axis of the loop.
-
Magnitude of force of interaction between two dipoles of moments and is given by where is the distance between them.
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The field due to the bar magnet can be written as B = 2 π x 3 μ 0 M . Hence flux through the ring is given by ϕ = B . A . cos 0 = 2 π x 3 μ 0 M π a 2 = 2 x 3 μ 0 M a 2 .
Thus using the Laws for Electromagnetic Induction, the induced current in the loop can be determined.
i = − R 1 . d t d ϕ ⇒ i = − R 1 . d t d ( 2 x 3 μ 0 M a 2 ) i = − 2 R μ 0 M a 2 ( − x 4 3 . d t d x ) ⇒ i = 2 R x 4 3 μ 0 M a 2 v
Using formula for the field due to a circular current carrying loop, we get,
B loop = 2 ( a 2 + x 2 ) 3 / 2 μ 0 i a 2 = 2 x 3 μ 0 a 2 ( 2 R x 4 3 μ 0 M a 2 v ) = 4 R x 7 3 μ 0 2 M a 4 v
For the force of interaction we will not use the mentioned formula because the magnetic moments are varying and not constant . The formula is actually only for constant moments M 1 and M 2 . Hence,
F = − d x d ( − M . B loop )
⇒ F = d x d ( 4 R x 7 3 μ 0 2 M 2 a 4 v ) ⇒ ∣ F ∣ = 4 2 1 . R x 8 μ 0 2 M 2 a 4 v . Add the required values to get the answer.
NOTE: I have deliberately given the formula to bring out the importance of the question and the validity of the formula.