Not your everyday wire
In this problem we deal with a wire that not
ideal
.
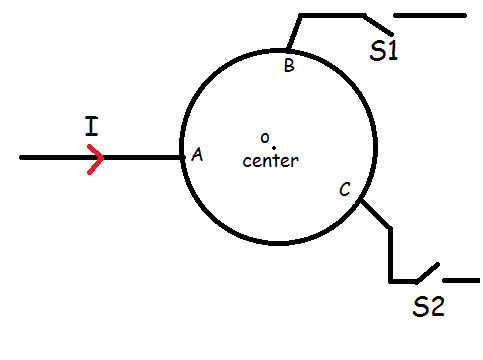 The circuit is made of a wire shaped as a circle. A current of value
passes through the first part of the wire (before it reaches the circular part). At first,
is turned on and a magnetic flux density of value
is created in the center of the circle (assume that the magnetic flux is created only by the circular part). After this,
is switched off and
is turned on. Now we get another magnetic flux density of value
.
The circuit is made of a wire shaped as a circle. A current of value
passes through the first part of the wire (before it reaches the circular part). At first,
is turned on and a magnetic flux density of value
is created in the center of the circle (assume that the magnetic flux is created only by the circular part). After this,
is switched off and
is turned on. Now we get another magnetic flux density of value
.
Find the the sum of and give your answer to two decimal places.
Note: The and .
The answer is 0.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is stated that the wires are not ideal.which means that they have a constant resistance per unit lenght
In the 1st case when S 1 is turned on the current after reaching point A finds two paths with different resistance.. If path A B has a resistance R then path A C B has a resistance 3 R as it is 3 times longer than A B
So the current through A B , I A B = 4 3 I
And the current through A C B , I A C B = 4 1 I
Now the magnetic flux intensity created by the A B part in the center can be given by-
B A B = ∫ 0 2 π 4 π r μ I A B d θ
B A B = 3 2 r 3 μ I
Now again the magnetic flux intensity created by the A C B part can be given by-
B A C B = ∫ 0 2 3 π 4 π r μ I A C B d θ
B A C B = 3 2 r 3 μ I
So it seems that B A B = B A C B But if we use the right hand rule we find that B A B and B A C B have opposite direction
So, B 1 = B A B − B A C B
B 1 = 0
In the same way we would find that B 2 = 0
So, B 1 + B 2 = 0 . 0 0
A n s w e r : 0 . 0 0
The two decimal places were just there to throw you off... :3