An ellipse, a line, and an inscribed circle
You are given the ellipse
4 9 x 2 + 1 6 y 2 = 1
and the line y = 2 x . You want to place a circle in the right half Cartesian plane, such that it is tangent to the ellipse at two points and to the line at a third point. This is shown in the figure below. Find the radius R of this circle and enter ⌊ 1 0 0 0 R ⌋ .
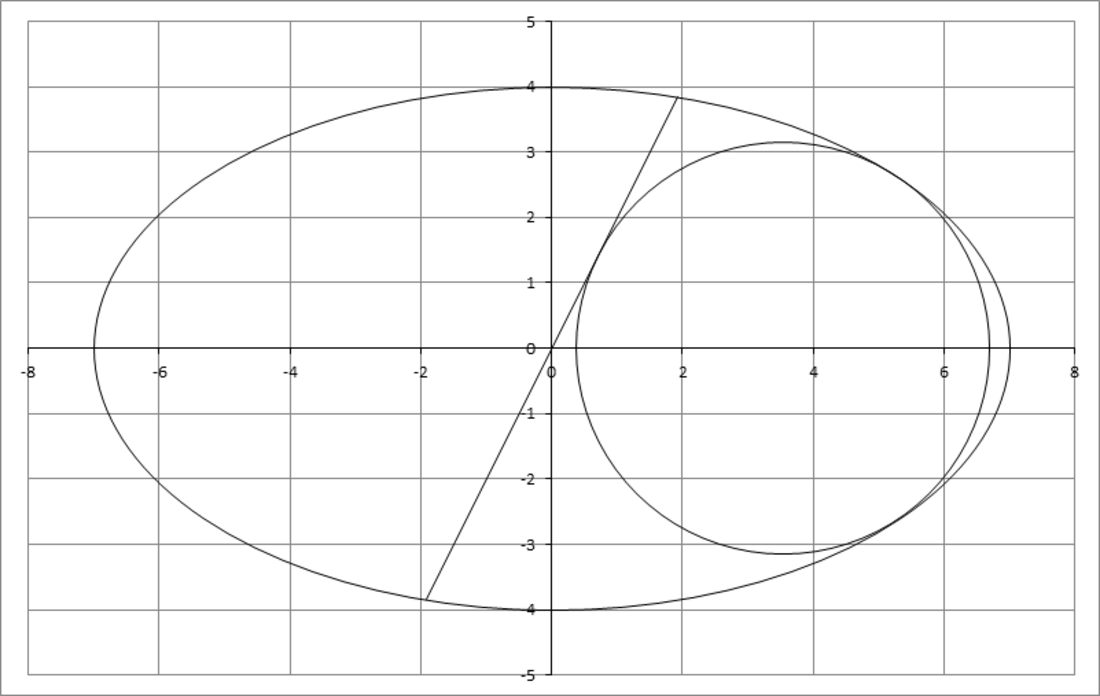
The answer is 3156.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
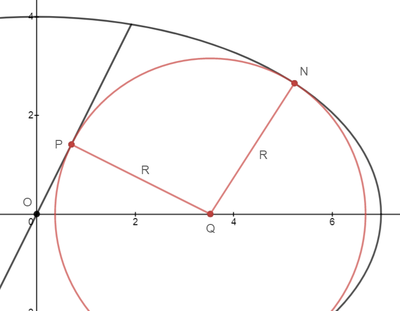
Let the centers of the ellipse and the circle be O ( 0 , 0 ) and Q ( x Q , 0 ) , and the points the circle is tangent to y = 2 x and the ellipse be P and N respectively..
As tan ∠ P O Q = 2 , O Q = P Q ⋅ csc ∠ P O Q ⟹ x Q = 2 5 R . Then the equation of the circle and its gradient at a point ( x , y ) are:
( x − 2 5 R ) 2 + y 2 2 ( x − 2 5 R ) + 2 y d x d y ⟹ d x d y = R 2 = 0 = − y x − 2 5 R . . . ( 1 a ) . . . ( 1 b )
Similarly,
4 9 x 2 + 1 6 y 2 4 9 2 x + 1 6 2 y ⋅ d x d y ⟹ d x d y = 1 = 0 = − 4 9 y 1 6 x . . . ( 2 a ) . . . ( 2 b )
At R , we have ( 1 a ) = ( 2 a ) and ( 1 a ) = ( 2 b ) .
( 1 b ) = ( 2 b ) : − y x − 2 5 R = − 4 9 y 1 6 x ⟹ x = 6 6 4 9 5 R
1 6 × ( 2 a ) − ( 1 a ) : 5 R x − 4 5 R 2 R 2 ⟹ R ⌊ 1 0 4 R ⌋ = 1 6 − R 2 = 5 3 1 6 × 3 3 = 4 5 3 3 3 ≈ 3 . 1 5 6 3 0 5 4 5 9 0 7 = 3 1 5 6 Note that x = 6 6 4 9 5 R
Label the diagram as follows:
Since the line has a slope of 2 , O B A B = 2 , and since △ O A C ∼ △ O B A by AA similarity, O B A B = O A A C , or 2 = O A R , which solves to O A = 2 1 R .
By the Pythagorean Theorem on △ O A C , O C = R 2 + ( 2 1 R ) 2 = 2 1 5 R .
The circle then has an equation of ( x − 2 1 5 R ) 2 + y 2 = R 2 , so y 2 = R 2 − ( x − 2 1 5 R ) 2 .
Substituting this into the ellipse equation 4 9 x 2 + 1 6 y 2 = 1 and solving for x gives x = 6 6 7 ( 7 5 R ± 2 5 3 R 2 − 5 2 8 ) .
Since the circle is tangent to the ellipse, there should only be one x value, so the discriminant 5 3 R 2 − 5 2 8 = 0 , and this solves to R = 4 5 3 3 3 .
Therefore, ⌊ 1 0 0 0 R ⌋ = ⌊ 4 0 0 0 5 3 3 3 ⌋ = 3 1 5 6 .