An Enginner Cannot Reproduce This Problem
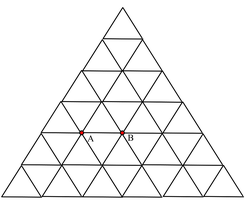 Alice has a box with many identical
resistors and she decides to arrange them in an infinite triangular lattice (a portion is shown in the above figure). She is interested in the electrical properties of this triangular mesh. She uses an Ohmmeter to determine the equivalent resistance between points A and B.
Alice has a box with many identical
resistors and she decides to arrange them in an infinite triangular lattice (a portion is shown in the above figure). She is interested in the electrical properties of this triangular mesh. She uses an Ohmmeter to determine the equivalent resistance between points A and B.
What is the Ohmmeter's in Ohms reading?.
The answer is 0.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The problem can be solved by superposition.
Inject I current at point A. There are 6 branches at A and hence by symmetry, each branch will carry a current of I/6 This is the first case.
Now remove I current from point B. Using the same argument as above, the branch AB carries a current of I/6
Superpose the above cases. Hence effectively the branch AB carries a current of I/3
The resistance of AB is 1 hence the resistance of the remaining circuit is 0.5
AB and the remaining circuit are in parallel and hence the equivalent resistance is 0.333