An Even Challenge
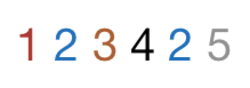 How many numbers of Six digits can be made by arranging the digits of the number
so that all the even digits do not occupy consecutive places.
How many numbers of Six digits can be made by arranging the digits of the number
so that all the even digits do not occupy consecutive places.
Details and Assumptions
- The number is indeed , there is no typo.
Solve more problems like this in my set Combinatorics .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The total number of possible six digit numbers that can be formed using the digits 1,2,2,3,4,5 is given by 2 ! 6 ! = 3 6 0 Now, to find out the number of cases in which all the even digits are consecutive, we consider the digits 2,2 and 4 as one group. The total number of elements now is 4. 2 2 4 1 3 5
The possible cases is given by 2 ! 4 ! × 3 ! = 7 2
Therefore, the final result 3 6 0 − 7 2 = 2 8 8