An Exercise in Solid Angle Computation
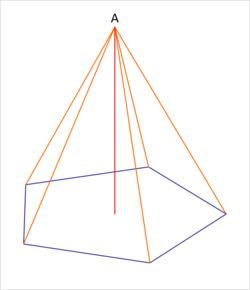 A pentagon lies in the XY plane centered at the origin. The pentagon is inscribed within a circle of radius equal to
units. Point A lies on the z-axis,
units from the center of the pentagon. If the solid angle subtended by the pentagon at the point A is given by
, what is
, correct to 3 decimal places ?
A pentagon lies in the XY plane centered at the origin. The pentagon is inscribed within a circle of radius equal to
units. Point A lies on the z-axis,
units from the center of the pentagon. If the solid angle subtended by the pentagon at the point A is given by
, what is
, correct to 3 decimal places ?
The answer is 0.1657.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
simple brute force: let A be (0, 0, 10) and two vertices on pentagons are (5, 0, 0) and (5cos(2π/5), 5sin(2π/5), 0)
we need to find angle between vectors (-5, 0. 10) and (-5cos(2π/5), -5sin(2π/5), 10) which is arccos((25cos(2π/5) + 100)/(25 + 100))
after simplification we have the answer: arccos((cos(2π/5) + 4)/5)/π = 0.169, not 0.166 as provided