This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Mark Hennings - Nice Solution!!
@Mark Hennings For the case of n = 3 we split the integral into two integrals each repeated 3 times thus making a total 3 ! cases which is what we expect when we rearrange all possible variants of the inequality 0 < x < y < z < 1 . That is ,
∫ 0 1 ∫ 0 1 ∫ 0 1 { y x } { z y } { x z } d x d y d z = 3 1 fractional part 0 < x < y < z < 1 ∫ y x z y { x z } d x d y d z + 3 2 fractional parts ∫ 0 < x < z < y < 1 y x { z y } { x z } d x d y d z
Exploiting symmetry for the case n = 4 in a similar manner we see that there will be three such splits of integrals with different coefficients having 1 , 2 , 3 fractional parts respectively. If we consider a n to be coefficient of such a split integral having n fractional parts in it's respective region of integration.
For the case n = 3 it seems that a 1 = a 2 = 3 , for the case of 4 integrals a 1 = 4 , a 2 = 1 6 , a 3 = 4 where ultimately all the a i 's if added will definitely produce m ! where m is the dimension of the integral we are working on since m variables can be rearranged in m ! ways 0 < x 1 < x 2 < ⋯ < x m < 1 .
Since it seems quite impossible for me to identify a pattern of those coefficients. For the case of 5 integrals , the integral will be divided into 4 subintervals where a 1 = 5 , a 2 = 5 5 and so on. So it comes to me that we need a way to solve for those coefficients. This problem is equivalent to :
How many ways are there to rearrange 0 < x 1 < 2 < ⋯ < x n < 1 so that out of these n fractions x 2 x 1 , x 3 x 2 , ⋯ , x 1 x n exactly k < n of them will be > 1 .
Is there a way to approach this ? I am thinking of this from a pretty long time
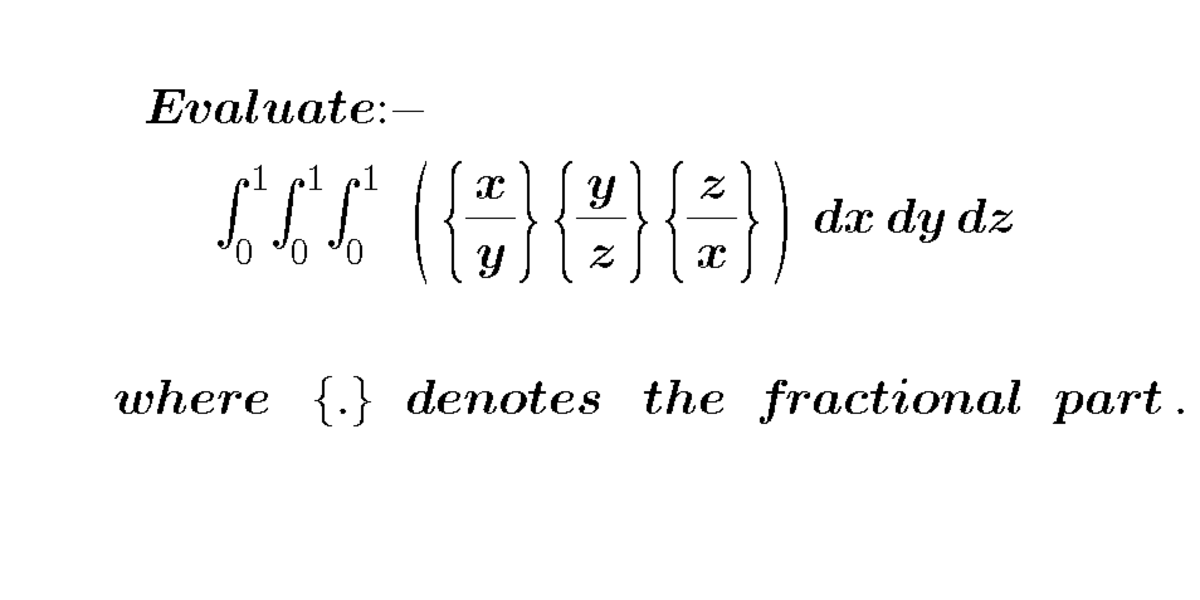
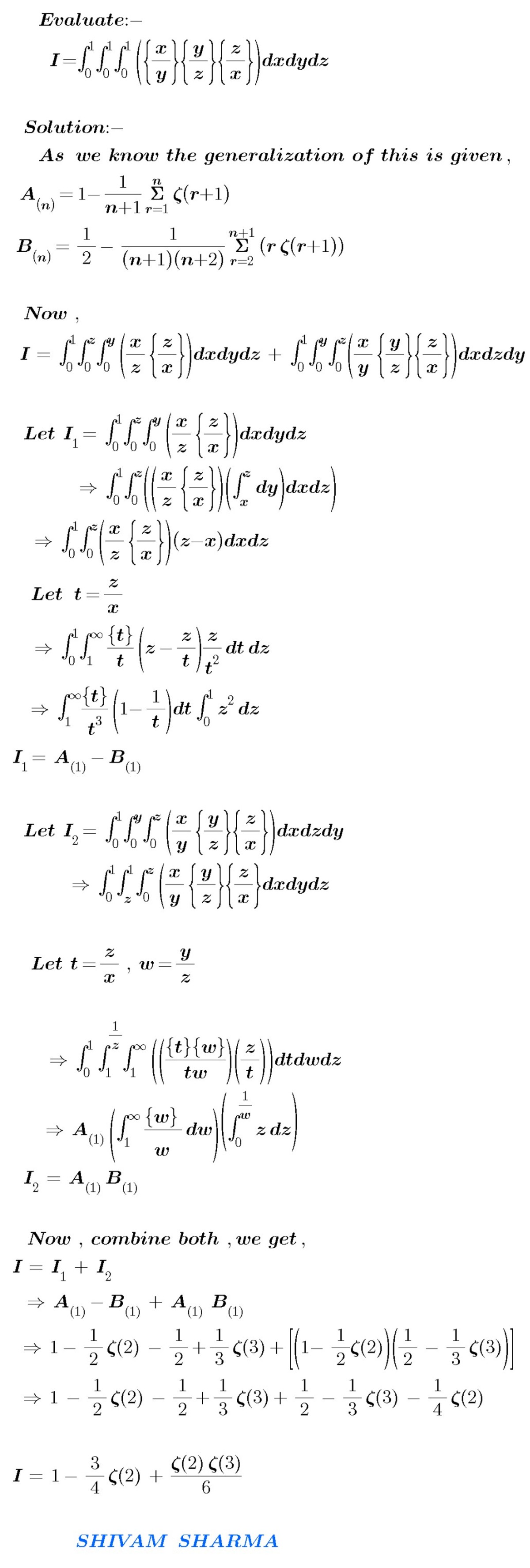
By methods analogous to those shown here , and doubtless elsewhere, we can show that ∫ 0 1 ∫ 0 1 ∫ 0 1 { y x } { z y } { x z } d x d y d z = A 1 − A 2 + A 1 A 2 where A j = ∫ 0 1 t j { t − 1 } d t j ≥ 1 We then calculate A j = ∫ 0 1 t j { t − 1 } d t = ∫ 1 ∞ u − j − 2 { u } d u = k = 1 ∑ ∞ ∫ k k + 1 ( u − k ) u − j − 2 d u = k = 1 ∑ ∞ [ j 1 ( k j 1 − ( k + 1 ) j 1 ) + j + 1 k ( ( k + 1 ) j + 1 1 − k j + 1 1 ) ] = j 1 − j + 1 1 ζ ( j + 1 ) and so the integral is 1 − 4 3 ζ ( 2 ) + 6 1 ζ ( 2 ) ζ ( 3 ) = 1 − 8 1 π 2 + 3 6 1 π 2 ζ ( 3 ) = 0 . 0 9 5 8 5 0 1 7 4 9 1