An Infinite Sum of Fractions
2 x + 8 x + 3 2 x + 1 2 8 x + … = 1 8 , x = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
2 x ∗ 1 − 2 2 1 1 = 3 2 x = 1 8 x = 2 7
S ∞ = 1 − r a 1 8 = 1 − 4 1 2 x 1 8 = 4 3 2 x 1 8 = 2 3 x x = 2 7
I used common sense I don't have a mathematical knowledge base to solve this. The fact that this is multiple choice allowed me to find the answer.
As the denominator gets bigger the number itself gets smaller. The first number is x/2 so I need to find something close to 18 to feel comfortable making an educated guess. 3 and 9 don't come anywhere close to 18. 18/2 is 9 and 18/8 is 2.25 but that isn't really there either.
27/2= 13.5 and 27/8=3.375. With those together they make 16.875. This answer provides a logical asumptiom that as the number gets smaller you get closer to 18. My educated guess is then 27.
Yay for us uneducated folks!
Other than knowing the formula for the sum of an infinite geometric series, another simple solution to this problem goes with the usage of the common ratio.
Factoring out 1/4 (which is the common ratio) from the right side of the equation, plus a simple substitution: 4 1 [ 2 x + ( 2 x + 8 x + 3 2 x + . . . ) ] = 1 8 4 1 [ 2 x + ( 1 8 ) ] = 1 8 2 x + 1 8 = 7 2 2 x = 5 4 x = 2 7 .
(x/2)(1 + 1/4 + 1/16 + ........ ) = 18
1/(1 - 1/4) = 36/x
x = 27
x/2+ x/8+ x/32+....=18
=>x/2(1+ 1/4+ 1/16+....)=18......... Statement(1)
Now, 1+ 1/4+ 1/16... is an infinite series with first term 1 and difference between two terms of 1/4
Hence 1+1/4+1/16+....=1/(1-1/4)=4/3
Hence statement(1) can be rewritten as
x/2*4/3=18
On simplifying x= 27
If you divide the LHS by 4, you get the same minus the 2 x at the beginning. This instantly reduces the problem to solving 2 x + 4 1 8 = 1 8
S(inf) = a1/1-r 18=x/2 / 1-1/4 18= x/2 / 3/4 18= x/2 *4/3 18= 2x/3 9= x/3 27=x x=27
Take x common, the series left us an infinite geometric progression with first term a= 1/2 and common ratio r =1/4. Use formula for summation of infinite g.p. : a÷(1-r)
Notemos que, a sequência é um P.G cuja razão vale 4 1 .
Com isso,
S n = 1 − q a 1 1 8 ⋅ ( 1 − 4 1 ) = 2 x 2 x = 1 8 ⋅ 4 3 x = 9 ⋅ 3 x = 2 7
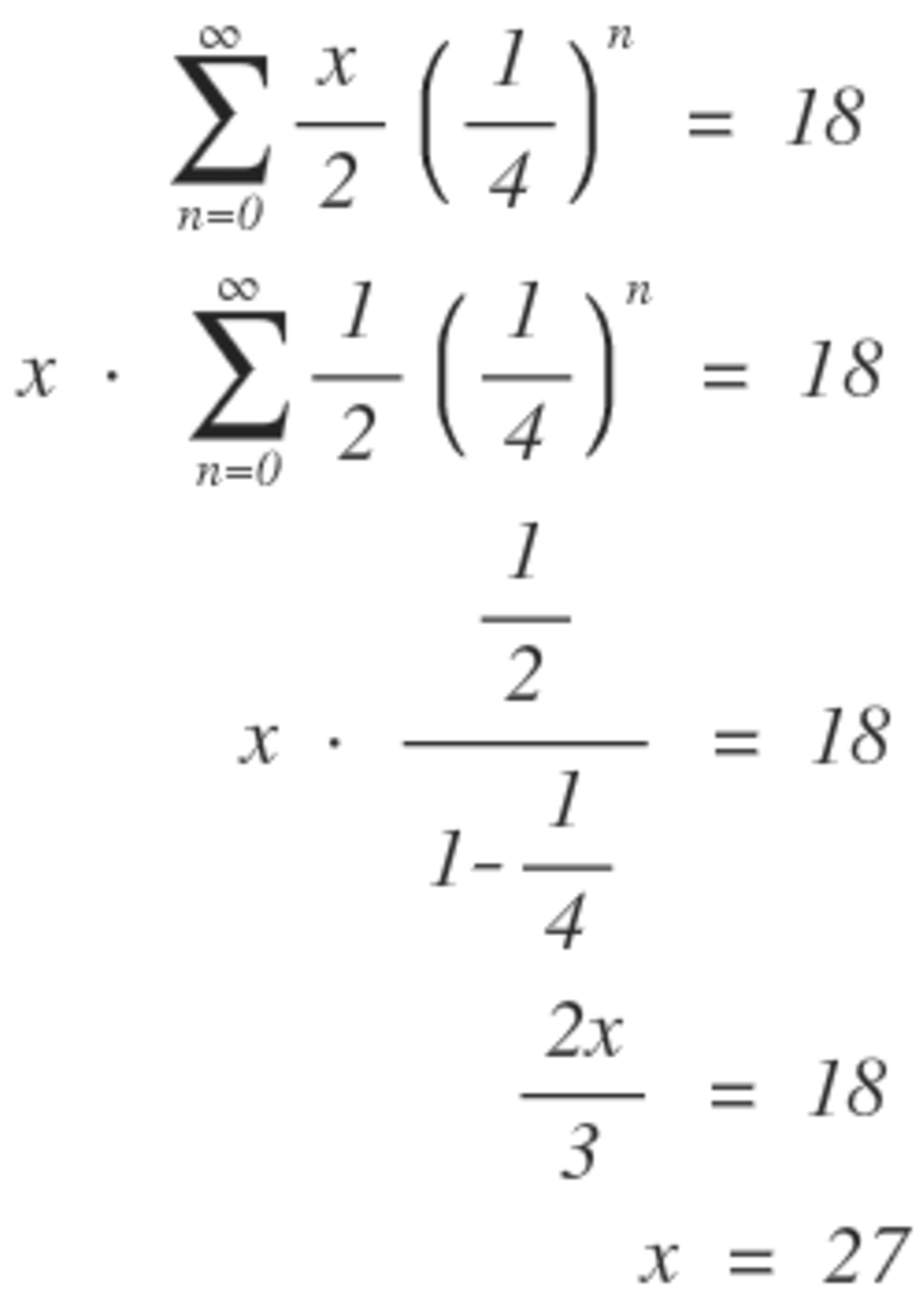
x + 4 x + 4 2 x + . . . = 3 6 = 1 − 4 1 x ⇒ 3 4 x = 3 6 ∴ x = 2 7