An Inscribed Equilateral Triangle

Let $X$ be the area of $\triangle CDF$ , $Y$ be the area of $\triangle ADE$ , $Z$ be the area of $\triangle BEF$ , $x$ be the side of the equilateral triangle, and $\theta$ be $\angle CDF$ .

Since $ABCD$ is a rectangle, $\angle ADC = \angle DCB = 90°$ , and since $\triangle DEF$ is an equilateral triangle, $\angle EDF = \angle DFE = 60°$ .

Since $\angle ADE$ $=$ $\angle ADC - \angle EDF - \angle FDC$ , $\angle ADE$ $=$ $90° - 60° - \theta$ or $\angle ADE\ = 30° - \theta$ .

Since the angle sum of a $\triangle CDF$ is $180°$ , $\angle DFC$ $=$ $180° - \angle DCF - \angle CDF$ $=$ $180° - 90° - \theta$ or $\angle DFC = 90° - \theta$ .

And since $\angle BFC$ is a straight angle, $\angle BFE$ $=$ $180° - \angle CFD - \angle DFE$ $=$ $180° - (90° - \theta) - 60°$ or $\angle BFE = 30° + \theta$ .

From $\triangle CDF$ , $CD = x \cos \theta$ and $X = \frac{1}{2}x \cdot x \cos \theta \cdot \sin \theta$ or $X = \frac{1}{4}x^2 \sin 2\theta$ .

From $\triangle ADE$ , $AD = x \cos (30° - \theta)$ and $Y = \frac{1}{2}x \cdot x \cos (30° - \theta) \cdot \sin (30° - \theta)$ or $Y = \frac{1}{4}x^2 \sin 2(30° - \theta)$ .

From $\triangle BEF$ , $BF = x \cos (30° + \theta)$ and $Z = \frac{1}{2}x \cdot x \cos (30° + \theta) \cdot \sin (30° + \theta)$ or $Z = \frac{1}{4}x^2 \sin 2(30° + \theta)$ .

Then $Z - Y$

$= \frac{1}{4}x^2 \sin 2(30° + \theta) - \frac{1}{4}x^2 \sin 2(30° - \theta)$

$= \frac{1}{4}x^2 (\sin 2(30° + \theta) - \sin 2(30° - \theta))$

$= \frac{1}{4}x^2 (\sin (60° + 2\theta) - \sin (60° - 2\theta))$

$= \frac{1}{4}x^2 \cdot 2 \cdot \frac{\sin (60° + 2\theta) - \sin (60° - 2\theta)}{2}$

$= \frac{1}{4}x^2 \cdot 2 \cdot \cos 60° \sin 2\theta$

$= \frac{1}{4}x^2 \sin 2\theta$

$= X$

Therefore, if $Z = 50$ and $Y = 30$ , $X = Z - Y = 50 - 30 = \boxed{20}$ .

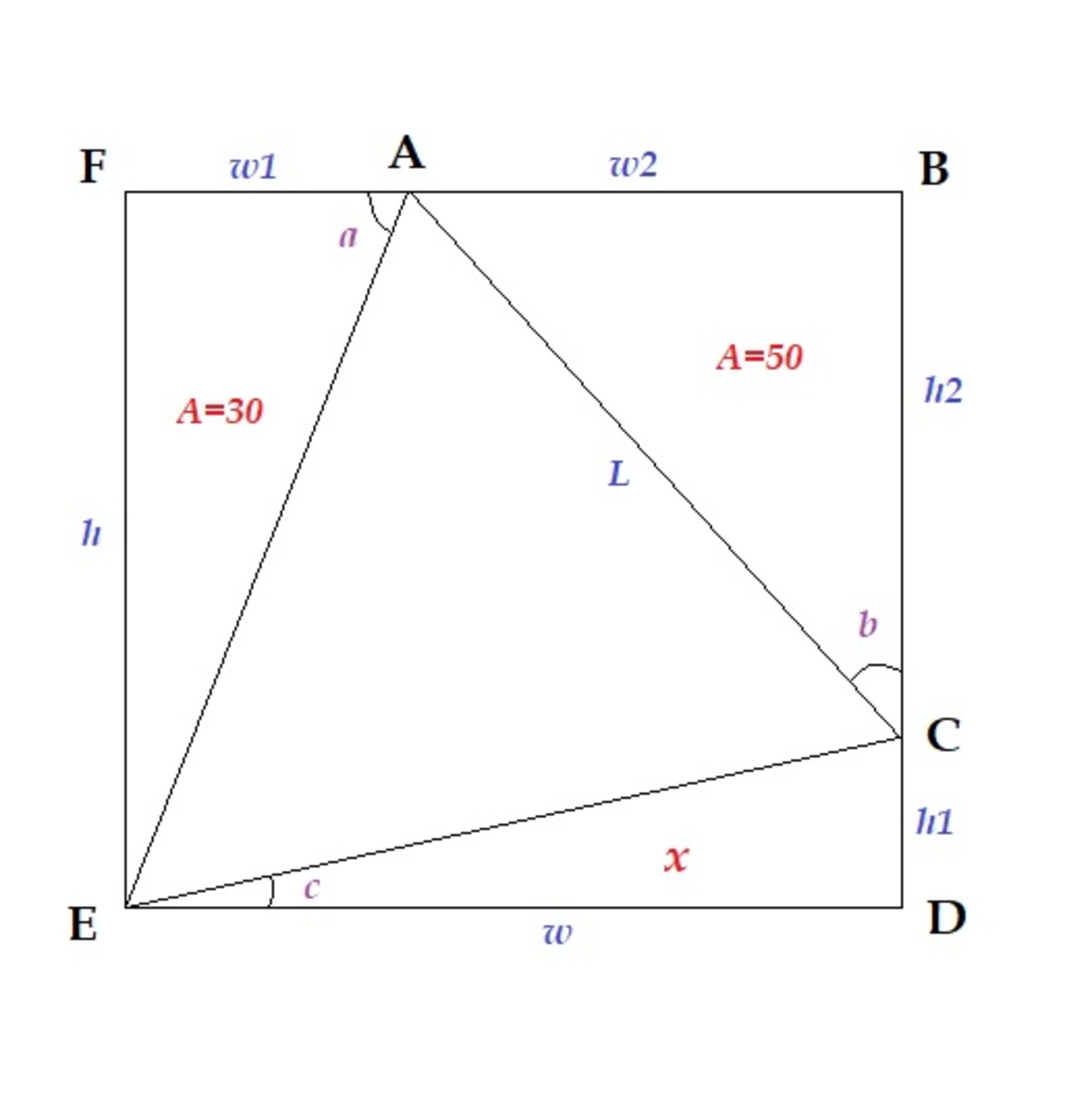
Starting with angle relationships:

At point A: $a + \frac{\pi}{3} + \frac{\pi}{2} - b = \pi \Rightarrow a-b = \frac{\pi}{6}$ .

Similarly, $b-c = \frac{\pi}{6} \space and \space a-c = \frac{\pi}{3}$ .

Now with segment lengths relationships: Let $L$ be the length of the side of the equilateral triangle; its area is $L^2 \frac{\sqrt{3}}{4}$ . Let $w$ and $h$ be the rectangle's width and height, respectively, and $w_1, w_2, h_1, h_2$ the subdivided width and height where the rectangle intersects the triangle, with: $w=w_1+w_2 \space and \space h=h_1 + h_2$

Given that the three outer triangles are rectangle, we have:

$\scriptstyle w_1 = L \cos a \space; \space w_2 = L \sin b \space; \space w=L \cos c \space ; \space h_1 = L \sin c \space ; \space h_2 = L \cos b \space; \space h=L \sin a$

Surface area of $ABC = w_2 h_2 / 2 = 50 \Rightarrow \frac{L^2 \sin b \cos b}{2} = \frac{L^2 \sin 2b}{4} = 50 \Rightarrow L^2= \frac{200}{\sin 2b} (I)$

Surface area of $AEF = w_1 h / 2 = 30 \Rightarrow \frac{L^2 \sin a \cos a}{2} = \frac{L^2 \sin 2a}{4} = 30 \Rightarrow L^2= \frac{120}{\sin 2a} (II)$

Surface area of $EDC: x = h_1 w/2 = \frac{L^2 \sin c \cos c}{2} = \frac{L^2 \sin 2c}{4} (III)$

$\scriptstyle Equations (I) \space and \space (III) \Rightarrow$ $x= \frac{200}{\sin 2b}.\frac{\sin 2c}{4} = 50 \frac{\sin 2c}{\sin 2b}$ $= 50 \frac{\sin (2b - \frac{\pi}{3})}{\sin 2b} = 50 \frac{\sin 2b.\cos \frac{\pi}{3} - \cos 2b.\sin \frac{\pi}{3} }{\sin 2b} = 25 - 25\sqrt{3} \frac{\cos 2b}{\sin 2b}$

$\scriptstyle Equations (I) \space and \space (II) \Rightarrow$ $\frac{200}{\sin 2b} = \frac{120}{\sin 2a} \Rightarrow \frac{3}{5} = \frac{\sin 2a}{\sin 2b} \Rightarrow \frac{\sin (\frac{\pi}{3} + 2b)}{\sin 2b}$ $= \frac{\sin \frac{\pi}{3} \cos 2b + \cos \frac{\pi}{3} \sin 2b}{\sin 2b} = \frac{\sqrt{3}}{2}.\frac{\cos 2b}{\sin 2b} + \frac{1}{2}$

$\Rightarrow \frac{3}{5} - \frac{1}{2} = \frac{\sqrt{3}}{2}.\frac{\cos 2b}{\sin 2b} \Rightarrow \frac{\cos 2b}{\sin 2b} = \frac{1}{5 \sqrt{3}}$

Consequently: $x= 25 - 25\sqrt{3}. \frac{1}{5 \sqrt{3}} = 25 - 5 = 20$

(That was a long way to prove that $x= 50-30$