An Inscribed Pentagon
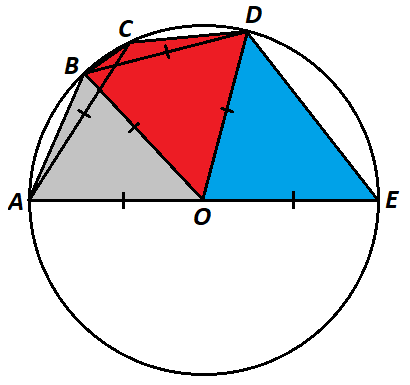
Pentagon is inscribed in circle such that is the diameter of circle and diagonals and are the same length as the radius of circle . If the red area is the area of quadrilateral and the blue area is the area of triangle , which area is larger?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let x be ∠ B O C and r be the radius of circle O . Since the sides of △ A O C are all equal to r , it is an equilateral triangle, and so ∠ A O C = 6 0 ° and ∠ A O B = ∠ A O C − ∠ B O C = 6 0 ° − x . Likewise, ∠ B O D = 6 0 ° and ∠ C O D = 6 0 ° − x . Since ∠ A O E is a straight angle, ∠ A O E = 1 8 0 ° , and ∠ D O E = ∠ A O E − ∠ A O B − ∠ B O C − ∠ C O D = 1 8 0 ° − ( 6 0 ° − x ) − x − ( 6 0 ° − x ) = 6 0 ° + x .
The red area is the combined area of triangles △ B O C and △ C O D , which is A r = 2 1 r 2 sin x + 2 1 r 2 sin ( 6 0 ° − x ) . The blue area is the area of △ D O E which is A b = 2 1 r 2 sin ( 6 0 ° + x ) . Then:
A r
= 2 1 r 2 sin x + 2 1 r 2 sin ( 6 0 ° − x )
= 2 1 r 2 ( sin x + sin ( 6 0 ° − x ) )
= 2 1 r 2 ( sin x + sin 6 0 ° cos x − cos 6 0 ° sin x ) )
= 2 1 r 2 ( sin x + sin 6 0 ° cos x − 2 1 sin x ) )
= 2 1 r 2 ( sin 6 0 ° cos x + 2 1 sin x ) )
= 2 1 r 2 ( sin 6 0 ° cos x + cos 6 0 ° sin x ) )
= 2 1 r 2 sin ( 6 0 ° + x )
= A b
Therefore, no matter what the value of x is, the red and blue areas are always equal.