An Inscribed Quadrilateral
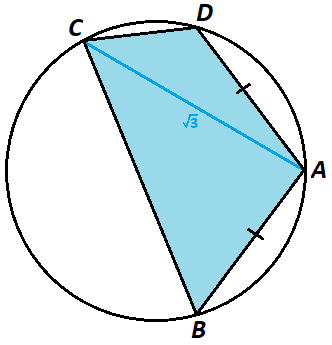
Quadrilateral is inscribed in a unit circle such that , , and diagonal . The perimeter of this quadrilateral can be expressed as , where and are integers. Find .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let O be the center of the unit circle. Then △ A C O has sides 1 , 1 , and 3 , and by the law of cosines ∠ A O C = 1 2 0 ° . Since an inscribed angle is half of the central angle of the same arc, ∠ A B C = 6 0 ° . Since opposite angles of a cyclic quadrilateral add up to 1 8 0 ° , ∠ A D C = 1 2 0 ° .
Method 1:
Let x = ∠ C O D . Then ∠ A O D = ∠ A O C − ∠ C O D = 1 2 0 ° − x . Since ∠ A O B and ∠ A O D are central angles that intercept congruent chords, ∠ A O B = ∠ A O D = 1 2 0 ° − x . Since a full revolution around point O is 3 6 0 ° , ∠ B O C = 3 6 0 ° − ∠ A O B − ∠ A O D − ∠ C O D = 3 6 0 ° − ( 1 2 0 ° − x ) − ( 1 2 0 ° − x ) − x = 1 2 0 ° + x .
Since the chord length c is related to the radius r and central angle θ by the equation c = 2 r sin 2 θ , C D = 2 ⋅ 1 ⋅ sin 2 x = 2 sin 2 x , B C = 2 ⋅ 1 ⋅ sin 2 1 2 0 ° + x = 2 sin ( 6 0 ° + 2 x ) , and A B = A D = 2 ⋅ 1 ⋅ sin 2 1 2 0 ° − x = 2 sin ( 6 0 ° − 2 x ) . Notice that:
B C
= 2 sin ( 6 0 ° + 2 x )
= 2 sin 6 0 ° cos 2 x + 2 cos 6 0 ° sin 2 x
= 2 sin 6 0 ° cos 2 x + sin 2 x
= 2 sin 6 0 ° cos 2 x − sin 2 x + 2 sin 2 x
= 2 sin 6 0 ° cos 2 x − 2 cos 6 0 ° sin 2 x + 2 sin 2 x
= 2 sin ( 6 0 ° − 2 x ) + 2 sin 2 x
= A D + C D
Therefore, the perimeter is P = A B + B C + C D + A D = ( A D ) + ( A D + C D ) + C D + A D = 3 ⋅ A D + 2 ⋅ C D , which means m = 3 and n = 2 , and 3 + 2 = 5 .
Method 2:
Reflect A B and C B in the perpendicular bisector of diagonal A C , so that B C ≅ A D , and A B > C D . (As reflection preserves length, this will not change the overall perimeter of quadrilateral A B C D .)
Since A C and A D are congruent opposite sides of a cyclic quadrilateral, A B and C D are parallel. Since consecutive angles of parallel lines are supplementary, ∠ B A D = 1 8 0 ° − ∠ A D C = 1 8 0 ° − 1 2 0 ° = 6 0 ° . Similarly, ∠ B C D = 1 8 0 ° − ∠ A B C = 1 8 0 ° − 6 0 ° = 1 2 0 ° . Therefore, quadrilateral A B C D is an isosceles trapezoid.
Let E be the intersection of A B and a perpendicular from C , and F be the intersection of A B and a perpendicular from D . Since A B and C D are parallel, C D F E is a rectangle, and E F = C D . From △ B C E , B E = B C cos 6 0 ° = 2 1 B C = 2 1 A D , and from △ A D F , A F = A D cos 6 0 ° = 2 1 A D . Therefore, A B = B E + E F + A F = 2 1 A D + C D + 2 1 A D = A D + C D .
Therefore, the perimeter is P = A B + B C + C D + A D = ( A D + C D ) + ( A D ) + C D + A D = 3 ⋅ A D + 2 ⋅ C D , which means m = 3 and n = 2 , and 3 + 2 = 5 .