An interesting construction
It is known that the A-series paper retains a ratio of 2 when folded in half lengthwise. However, other folds may yield interesting results of their own. Fold a piece of paper as such:
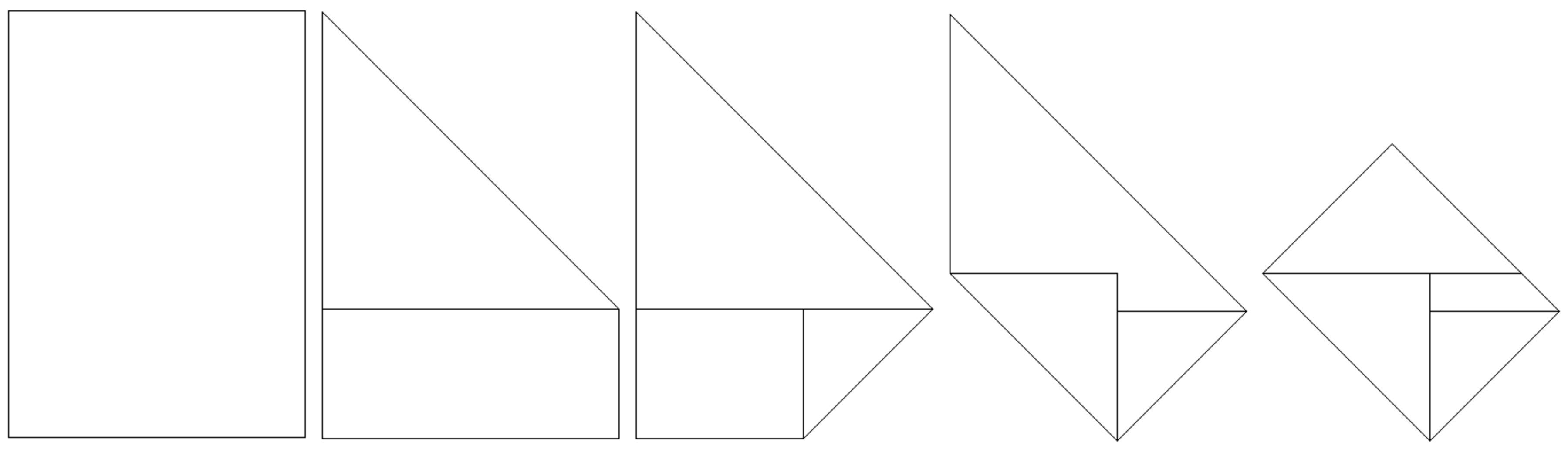
For which ratios of paper sizes are the final product also of the same ratio as the original? Enter your answer as the sum of all possible ratios.
The answer is 3.032.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
It is worth noting that in both ratios there are two solutions, i.e. for x y = 2 , there's also a solution x y = − 2 , and for x y = 2 1 + 5 , there is x y = 2 1 − 5 . However, since the two alternate solutions are negative, and the ratio is between two positive values and is thus necessarily positive, they are both rejected.
Log in to reply
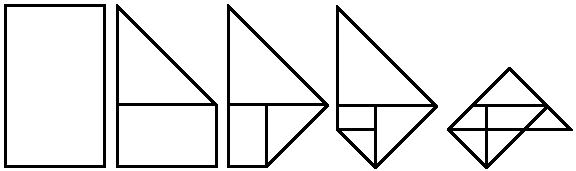
I want to add something. For the ratio of 2 1 + 5 , following the folding pattern doesn't return a rectangle.
Do we get a rectangle when the ratio is 2 1 + 5 ?
Yes, for a rectangle with a ratio of 2 1 + 5 , I suppose one more fold would be necessary to make it a rectangle with the same ratio as its original:
Log in to reply
Yes, that's the problem. One more fold is necessary.
Let rectangle A B C D be the paper with a width of x and a length of y so that A B = C D = x and A D = B C = y . Let E be the intersection of folds on B C , F be the intersection of folds on C D , and G be the intersection of folds on A D .
From the first fold we have B E = A B = x , and from the second fold we have C F = C E = B C − B E = y − x , and from the third fold we have D G = D F = C D − C F = x − ( y − x ) = 2 x − y . Since triangles △ C E F and △ D G F are right isosceles triangles, E F = 2 ( y − x ) and F G = 2 ( 2 x − y ) .
For the ratio of the final product to be the same as the original, either x y = 2 ( y − x ) 2 ( 2 x − y ) or x y = 2 ( 2 x − y ) 2 ( y − x ) . The first solves to y = 2 x for a paper ratio of x y = 2 , and the second solves to y = 2 1 + 5 x for a paper ratio of x y = 2 1 + 5 .
Therefore, the sum of all possible ratios is 2 + 2 1 + 5 ≈ 3 . 0 3 2 .