An interesting geometry problem I found - 2

Geometry Level 1

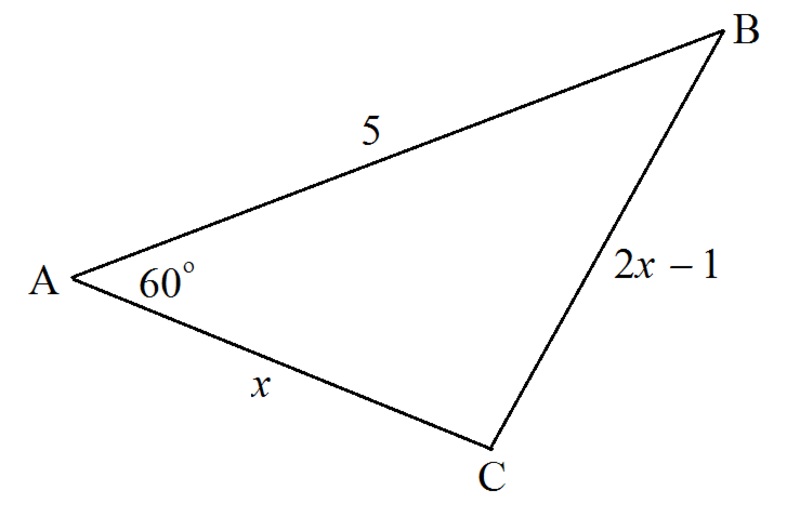
Triangle $ABC$ has sides of length $5$ , $x$ , and $2x-1$ . If $x$ is of the form $\dfrac ab$ , where $a$ and $b$ are positive coprime integers, find $a+b$ .

The answer is 11.

1 solution

Krishna Karthik
Nov 2, 2020

Note that this isn't an original problem and there are probably many like it; it was given to me as part of pre-IB advanced maths homework. We are getting taught the cosine rule now, but I solved this problem using vectors before I was taught the cosine rule.

I think this should show why learning vector algebra is very important; if you forget long formulas; you can always use a fundamental concept such as vectors.

Let the vectors that are on the lines $AB$ be $\vec{a}$ , $AC$ be $\vec{b}$ , and $BC$ be $\vec{c}$ .

We can deduce that $\displaystyle \vec{c} = \vec{a} - \vec{b}$ .

Furthermore, we know that the magnitude of vector $\vec{c}$ is $2x - 1$ .

$\vec{b} = \braket{x,0}$ , and the components of vector $\vec{a}$ can be found using trigonometry:

$\displaystyle \vec{a} = \braket{\frac{5}{2}, \frac{5 \sqrt{3}}{2}}$

Hence,

$\displaystyle \vec{c} = \braket{\frac{5}{2} - x,\frac{5 \sqrt{3}}{2}}$

Equating the magnitudes:

$\displaystyle 2x-1 = \sqrt{\left(\frac{5}{2} - x \right)^2 + \left(\frac{5 \sqrt{3}}{2} \right)^2}$

This reduces to the quadratic equation:

$3x^2 + x -24 = 0$

For which a useful value of $\boxed{\displaystyle x = \frac{8}{3}}$

What you've done there is derive the cosine rule using vectors :-). Using your notation, if you don't substitute values in at the beginning, what you have is $\begin{aligned} \vec{a}&=\left \langle AB\cos \angle BAC,AB\sin \angle BAC \right \rangle \\ \vec{b}&=\left \langle AC,0 \right \rangle \\ \vec{c}&=\left \langle AB\cos \angle BAC - AC,AB\sin \angle BAC \right \rangle \end{aligned}$

Equating the magnitudes,

$\begin{aligned} BC^2 &=(AB\cos \angle BAC - AC)^2+AB\sin \angle BAC \\ BC^2 &=AB^2 + AC^2 - 2AB\cdot AC \cos \angle BAC \end{aligned}$

Still, good derivation - if you ever forget the cosine rule in an exam you can still answer the questions!

Chris Lewis - 7 months, 1 week ago

Wow! I never thought that I proved the cosine rule like that; I was just focusing on the problem. Lmao. Thanks mate.

Krishna Karthik - 7 months, 1 week ago

According to your assumption, $\vec c$ is not $\vec a-\vec b$ , but $\vec b-\vec a$ .

A Former Brilliant Member - 7 months, 1 week ago

@Foolish Learner $\vec{c}$ has to be $\vec{a} - \vec{b}$ because of the half of the parallelogram formed by that triangle's two adjacent sides, $AB$ and $BC$ . Because of orienting $A$ at the origin and $AC$ lying on the $x-$ axis, it has to be a - b. I've written that in the solution.

Krishna Karthik - 7 months, 1 week ago

Bruh I just realised the problem statement got edited. Thanks Chew Seong-Cheong

Krishna Karthik - 7 months, 1 week ago

Nice! Contrived problems are just so... satisfying. :)

David Stiff - 2 months, 2 weeks ago

An interesting geometry problem I found - 2

The answer is 11.

1 solution

0 pending reports