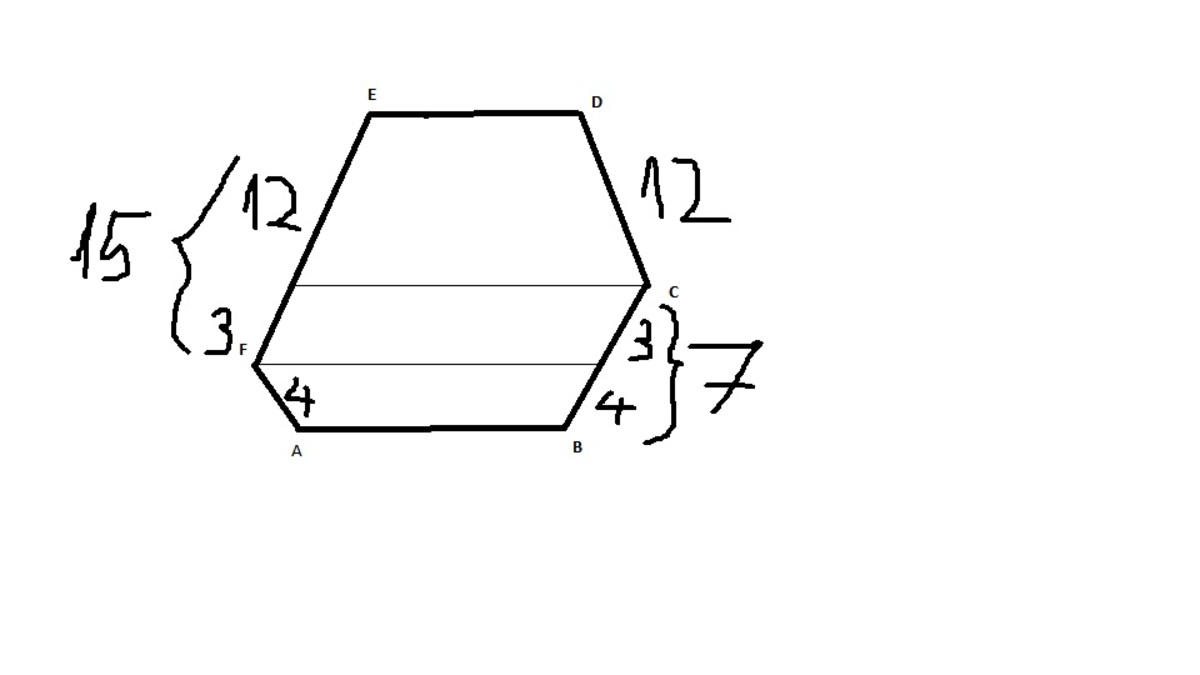
An interesting hexagon

As is obvious from the given picture, $\Delta PQR$ is equilateral. We can calculate the length of the required side without knowing one of the other sides, or to say we can derive the length of any two sides given the measure of the rest four sides( in the given configuration) /only.

One simple solution is to note that since all interior angles are equal, namely $120^\circ$ , then:

$FA + FE = BC + CD$ (since the absolute value of their slopes is equal if you take $AB$ to be flat)

or

$4+15 = 7 + ?$

$? = \boxed{12}$

Extend the sides measuring 10 and 18, and draw a rectangle such that the hexagon is inscribed in the rectangle. Being that each angle of a regular hexagon measures 120°, we now have four 30-60-90 triangles, as shown below.

Using the ratios for 30-60-90 triangles, we find the measures of the sides of these triangles, as demonstrated. AD is found by 15/2 √3+2√3 = 19/2 √3. BC = AD, so we find the missing segment of BC by 19/2 √3 - 7/2 √3 =6√3. Again using the ratios for 30-60-90 triangles, we find x = 12.

All interior angles are $120^{\circ}$ , so horizontal lines through the left and right extreme points make $60^{\circ}$ angles with the adjacent sides. Total horizontal travel from the extreme right point, moving clockwise around the figure, is therefore $-7/2 - 18 - 4/2 + 15/2 + 10 + x/2 = 0$ , so $x = 12$

The interior angles of an equiangular hexagon are each 120˚. This makes their exterior angles 60˚. If each side of the equiangular hexagon is used to make an equilateral triangle, the overall resulting shape is two large overlapping equilateral triangles (see figure below). In that figure, the highlighted sides of the two large equilateral triangles are completely determined and may be used to determine the unknown side length, x.

The congruent sides of the "downward" equilateral triangle are: (18 + 15 + 4) = (18 + 7 + x) = ( 15 + 10 + x).

The congruent sides of the "upward" equilateral triangle are: [15 + 10 + 4] = [18 + 7 + 4] = [10 + 7 + x]. 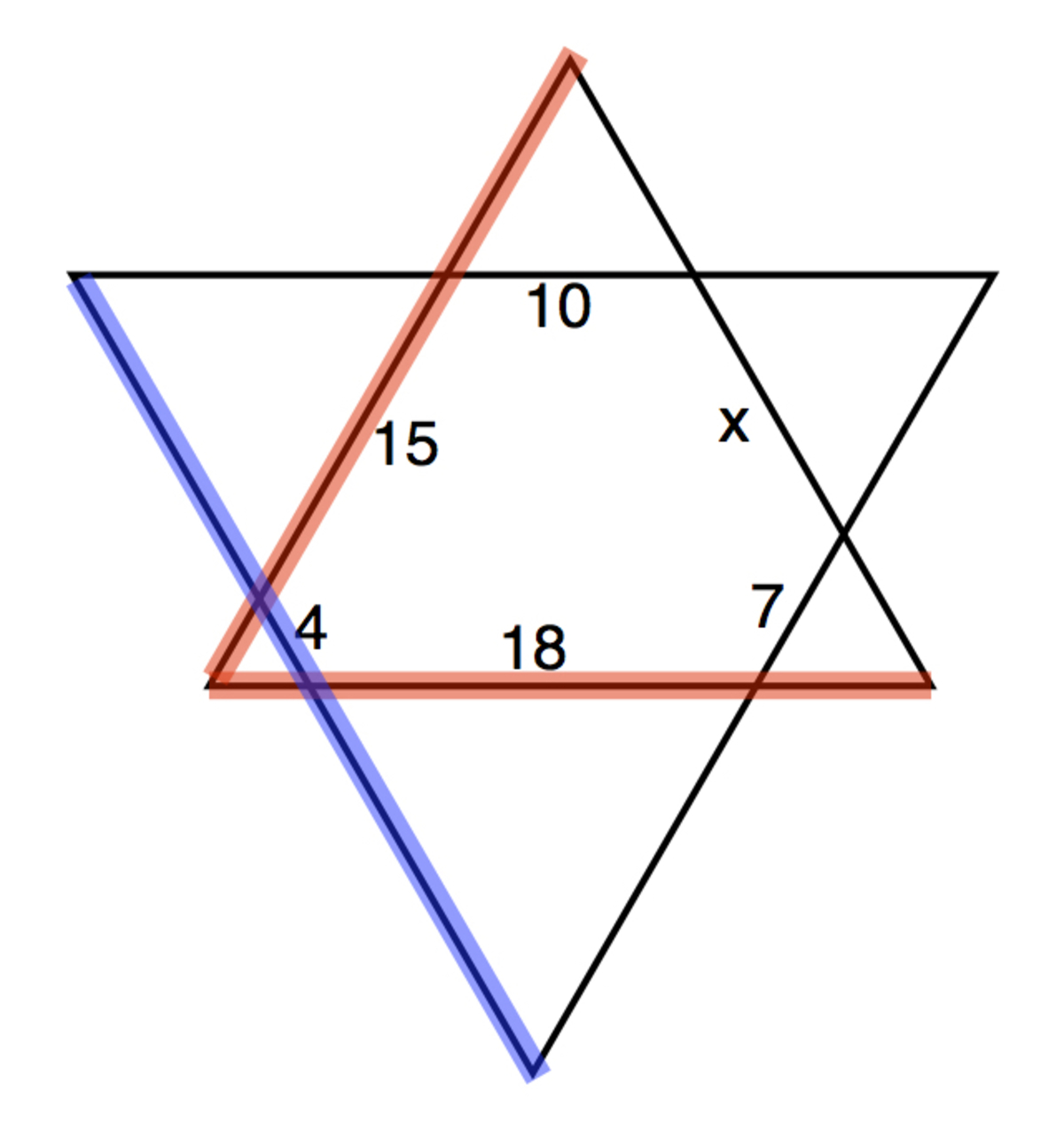(37) = (25 + x) is consistent with [29] = [17 + x] with the result that x = 12 .

ps. with a little imagination, it is possible to solve this problem with parallelograms. Try it!

A very simple solution is the following, since all angles are equal then the sum of its sides should be a multiple of 6. To the sum of the known sides only the addition of 12 (amongst the given figures) gives a multiple of 6. Indeed, 10+15+4+18+7+...12= 66.

Let the Unknown length is "x" Then using cosine rule 19^2 +22^2 - (2)(19)(22)cos60 = (10+x)^2 +(7+x)^2 - 2(10+x)(7+x)cos60. When this equation is simplified we get the quadratic equation x^2+17x-348=0. When this equation is solved we get x=12 or x=-29 So the acceptable answer is 12.

As In a hexagon length of opposite sides are equal i.e 15+4=x+7 19=x+7 X=19-7 X=12

Extend the sides marked 18, 15 and ? to get an equilateral triangle. Take a look at it and do the arithmetic :-)

I made a little GeoGebra applet to introduce this to people. https://www.geogebra.org/m/t93hTH3s

Love the problem, Áron!

Each side of the hexagone is drawn as a vector. The sum of all vectors must be zero. The unknown vector has a magnitud of 12

For this problem I just realized that to travel in a closed loop, the vector sum of all paths must be zero.

You can use symmetry to remove most of the work, take the difference between each pair of sides -- and realize they must be equal.

The known pairs come to 8, so the remaining difference must also be 8. Ergo - the length must be 12.

We really do not need the side 18 and that can be determined. To do so extend right, left, and bottom sides in both directions till you see you have an equilateral triangle, let the unknown side x and 18, y, then: 10 + 15 + 4 = 4 + y + 7 = 7 + x + 10, so y = 18, x = 12.

Interior Angles are found by (n-2) 180/n which yields 120 degree interior angles. You can then form right triangles on the left hand side using 30-60-90 degree triangles. The height of the 2 triangles will sum to 9.5 sq.rt. of 3. The triangle on the bottom right hand side has a height of 3.5 sq.rt. of 3 which means that the triangle on the top right hand side must have a height of 6 sq.rt. of 3. The length of the hypotenuse of this triangle is double the shortest side. The shortest side is 6 so the hypotenuse has to be 12.

Starting at the vertex between the lengths 18 and 7. If we only consider horizontal displacement, we are able to work out what horizontal displacement is missing and thus the magnitude of the length.

Working anticlockwise: -18 - 2 +7.5 +10 + X - 3.5 = 0 where a negative value is a displacement left, positive right. The minus 2 comes from a right angle triangle with a 60 degree angle (the first exterior) ... Cos 60 = a/4 ==> 0.5 x 4 = a.

If you use this for each of the 'diagonal' edges we are able to make the equation at the beginning of the previous paragraph. Leading to X = 6

For a horizontal displacement of 6, the magnitude would have to be 12.

I simply observed that the difference between each pair of opposite sides was eight units , so I simply guessed that the missing side was eight more than its opposite . If this were on a test of course, I would have double checked my work by drawing the three equilateral triangles and doing the work.

By seeing the diagram you can see all three parallel lines differ by 8 ie., 7+8=15,10+8=18 so,4+8=12 hence this is answer😎

Sides length 18 and 10 are parallel (Difference =8). So are sides 15 and 7 (Difference =8). Also sides ? and 4 (Difference = 8). Therefore ? =12

15/2 + 4 + 18/2 = 10/2 + x + 7/2, x = 12; not as good/simple as Rohit Camfar's answer.