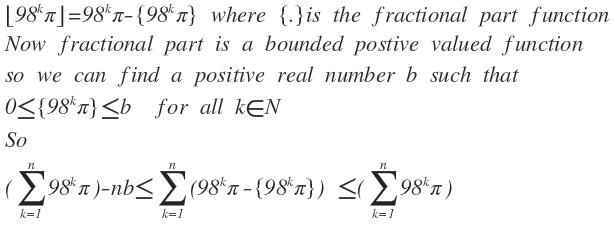An interesting limit involving floor function.
Find the following limit, if it exist. n → ∞ lim π 9 8 n + 1 ∑ k = 1 n ⌊ 9 8 k π ⌋ If the limit does not exist, enter the number 333 as your answer. If the limit exists but is an irrational number enter the number 111. In case that the limit is a rational number, it can be represented as b a , where a and b are coprime integer numbers. If this the case, enter the sum a + b .
Note: Here the expression ⌊ ⋅ ⌋ denotes the floor function .
The answer is 98.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let a be any number greater than 1, and x any real number.
We will start proving the following properties:
Property 1. lim n → ∞ a n + 1 − 1 ∑ k = 0 n ⌊ a k x ⌋ = a − 1 x .
Proof: Let us form the following difference: a − 1 x − a n + 1 − 1 ∑ k = 0 n ⌊ a k x ⌋ = x a n + 1 − 1 ∑ k = 0 n a k − a n + 1 − 1 ∑ k = 0 n ⌊ a k x ⌋ = a n + 1 − 1 ∑ k = 0 n ( a k x − ⌊ a k x ⌋ ) . Obviously, the expression obtained above is greater than or equal to zero and less than or equal to a n + 1 − 1 n + 1 . Then using the Sandwich theorem, we obtain that this difference as n → ∞ tends to zero and, therefore, the limit above is proven.
Property 2. lim n → ∞ x a n + 1 ∑ k = 1 n ⌊ a k x ⌋ = a − 1 1 .
Proof.
It is easy to obtain the Property 2 from Property 1 just by noticing that
x
a
n
+
1
∑
k
=
1
n
⌊
a
k
x
⌋
=
x
1
a
n
+
1
−
1
∑
k
=
0
n
⌊
a
k
x
⌋
a
n
+
1
a
n
+
1
−
1
−
x
a
n
+
1
⌊
x
⌋
.
So, the property 2 is also proven.
Now, we can use Property 2 to get limit given in this problem. By making a = 9 8 and x = π , and using the property, we obtain that the given limit is 9 7 1 . Therefore the answer to the question is 1 + 9 7 = 9 8 .