Tell me, do you?
h → 0 lim h ( 1 + h ) 1 2 3 4 5 6 7 8 9 − 1 = ?
The answer is 123456789.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
Great! The difference of powers formula is one way that we can differentiate polynomials easily!
Note: It helps to format your solution in a way that makes it friendly for people to read. I've made slight edits to improve it.
What are resources or tips I could use to improve my editing?
Let f ( x ) : = x 1 2 3 4 5 6 7 8 9 . By definition of derivative at x = 1 , f ′ ( 1 ) = x → 1 lim h ( 1 + h ) 1 2 3 4 5 6 7 8 9 − 1 . Therefore, x → 1 lim h ( 1 + h ) 1 2 3 4 5 6 7 8 9 − 1 = 1 2 3 4 5 6 7 8 9 .
When the value of h is put in the expression ,we get the expression in the form 0/0. So if we apply L hopitals rule , we get the expression in the form 123456789(1+h)^123456788 Applying limit we get answer as 123456789
This is a great problem, but seems like all the methods involve taking a derivative, but how would you do it if you have not derived the formula in the first place?
We note that ( 1 + h ) n = 1 + n h + 2 n ( n − 1 ) h 2 + . . . + h n
So subtracting 1 and dividing by h gives
n + terms with h , h 2 . . . h n − 1
Thus, taking h to zero gives n for sufficiently small h .
This represents the derivative of the function f ( x ) = x 1 2 3 4 5 6 7 8 9 at x = 1 so f ′ ( 1 ) = 1 2 3 4 5 6 7 8 9 ( 1 ) 1 2 3 4 5 6 7 8 9 − 1 = 1 2 3 4 5 6 7 8 9
The limit given can also be written as follows: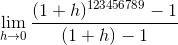 .
.
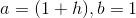 .
.
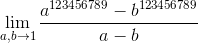 .
.
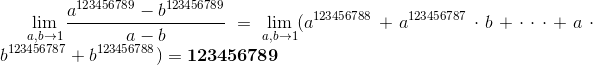
Given this, let
The limit can now again be rewritten as follows:
Using the difference of powers formula, we write this limit out again and complete the solution: