Infinite Radial Resistors
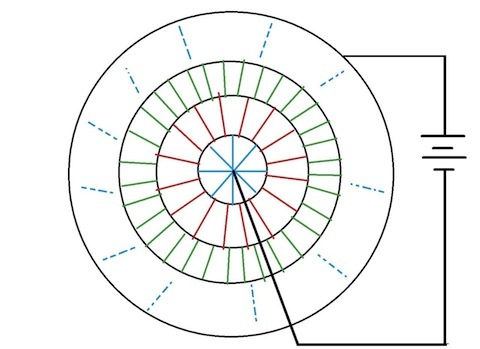 In the image, the black lines are connecting wires and colored lines are resistors of
each. The first circle contains 8 resistors, the second one contains 16, the third one contains 32, and so on. There are infinitely many circles of resistors.
In the image, the black lines are connecting wires and colored lines are resistors of
each. The first circle contains 8 resistors, the second one contains 16, the third one contains 32, and so on. There are infinitely many circles of resistors.
A cell is connected between the center and the outermost circle. The equivalent resistance in between the terminals of the cell is What is
Assume that the wires (black lines) have negligible resistance.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is clear from the diagram that,
All the resistors that have the same color, are in Parallel connection with each other (as the terminals are shorted out).
Hence, We can combine each same colored group into a single resistor.
For the first group,
R 1 1 = 1 1 + 1 1 + 1 1 + … 8 times = 8
⇒ R 1 = 8 1
Similarly, R 2 = 1 6 1 , R 3 = 3 2 1 , …
Now,
Clearly,
All of these resistors are in Series connection with one another.
Thus,
Final Resistance ( R ) = R 1 + R 2 + R 3 + …
⇒ R = 8 1 + 1 6 1 + 3 2 1 + …
⇒ R = 1 − 2 1 8 1
Hence,
R = k = 4 1
⇒ 1 0 0 k = 2 5